双列块法——大型、稀疏、对称线代数方程组的一种有效解法.pdf

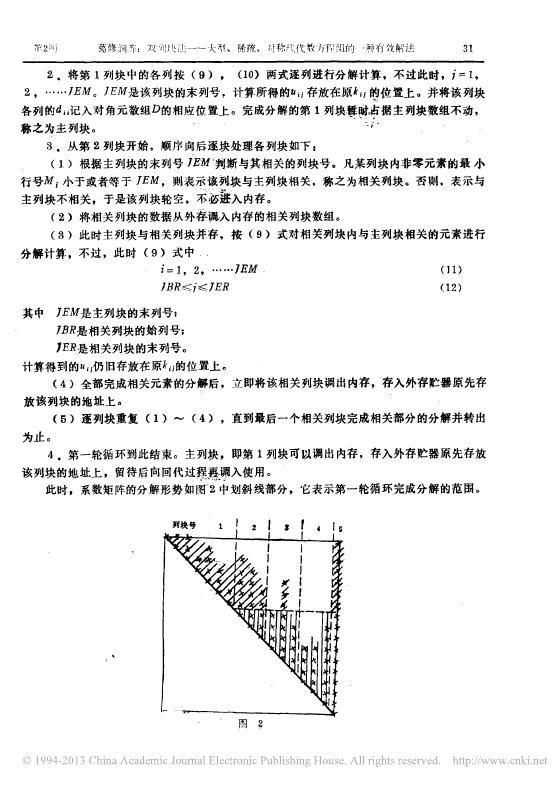
岩 土 第6 卷 第 2 期 l g as 年1 2 月 R o ek a d 5 0 11 M e e h n 、 o V 力 学 。 。 氏云 1 9 8 5 。 ie . an l 6 No 2 、 双 列 块 法 一 大 型 稀 疏 对 称线 代 数方 程 组 的 一 种 有 效解 法 葛修 润 杨家 岭 要 双 列 块 法 用于 有 限 元 分 析 计算 中求解 大 型 线 代 数 方 程 组 。 目 前 在有 限元 计算 中最 通 常 使 用 的求 解 大 型 线 代 数 方 程 组 的 方 法 是 分 块 的 三 角 分 解 法 这 种方 法对 方 程 组 系数 矩 阵的 分块 受 带 宽的限制 , 难 使 一 些 大 型 的 有 限 元 课 题 特 别是 三维问 题 的 解算 难 以 实 现 双 列 块 法对 方 程 组 系数 矩 阵实行按 计 算机 许 可 的容量划 分 列 块 。 宽 的 限制 方法是 成 功 的 , 夫半 带 宽 为 17 4 6 理元 、 83 1 、 。 有效 的 用双 列 块 法 在 P E 一 3 奢2 0 , 。 双 列块 法 解 决 了这 个困 按列 分解 可 以尧全 不 受 带 , 6 小 型机 上 仅 用 盼 K 字 节的 内存解 算了 最 系数矩阵 存 贮量 为 5 0 0 K 以上字节 的三 维 ( 12 召个2 0 个 节 点 )有 限 元 课题 由于 以 至 目 前 一般 计 算机 的 内 存贮 量 限制 了 大 带 宽 , 问 题 的 求解 。 ‘ 。 节点等参 元 ,8 扭 6 节 点等 参节 ‘ L , 这 种 方 法 使 小 型 和 高 档微 机 用 于 大 型有 限 元的 解算 成为 可 能 ‘ 、 用有 限 单 元 法 分 析 结构物 的 应 力 、 概 述 应 变 和 变位 时 通 过 物 理 近 似 和 离散 化 过 程 , 最 后 可将 问题 归 结 为求 解 一 个 线 代 数方程 组 K X 其 中系 数矩 阵 K 具 有 对 称 限元 分 析来 说 , 、 R = 、 (1 ) 正 定 稀 疏性 。 q 但 它 又 往 往 是 一 个 高 阶 的 矩 阵 对 于 大 型 问题 的 有 求解 上 述 方 程 组 的 计 算 时间 几 乎 占全 部 计 算 时 间 的 80 % 以上 所 需 占用 的 计 算机 内存 往往 最大 。 , 当 按 通 常采 用 的直 接 解法 来 求 解时 。 在 解方 程 时 , 虽 然充 分 利用 了 其 系 数 矩 阵 的 稀 疏对 称性 采 取 一 维 变带 宽 紧缩 存 贮 的 方 式 一 般 计 算机 内存 的 容 量 也 仍 旧难 以满 , , 足其 庞大 的 系 数矩 阵 的 存 贮 要 求 间 问 题 的有 限 元 分 析 计 算 时 求解 能力 的 一 个 关 键 问 题 年来 , , ’ , 。 随 着有 限 元 方 法 的 日 益 发 展 , 特别 在 对 于 大 型 结 构物 的 空 计 算 机 容 量 不 够 用 这 个 问题 就 更 为 突 出 , 以 致 成为 影 响 有 限 元 迫 使 从 事 有 限元 分 析 的 人 来 改 进 大 型 代 数方 程组 的 求 解 技 术 围 绕 着如 何 有 效 地 求 解 有 限 元 线 代 数 方 程 组 这 个 问 题 , 。 国 内外 都采 用 了 一 些 新 技 术 多 。 岩 土 这 些 新技 术的 一 个 共 同点就是 改 进算法 技巧 的 不 足 从 而 扩 大 了 计 算 机 的 容 纳 能力 , 、 非 零元 素 的 方法 等 充 分 利用 计 算 机 丰 富 的 外 部 存 贮 器 来 弥补 内 存 、 根 据 它 们使 用 不 同 的 矩 阵分解 方法 不 同 的 处理 矩 阵 数 据 在 计 算 机 内外 存 贮 器 不 同组 织 形 式 以及 不 同 的 内 外交 换技 术 各种 不 同 特 点 的 解 法 。 。 , 1 只8 5 年 学 力 例如 波前 法 [l] 。 、 、 超 元 矩 阵法 闭 带式 分 解 法 叫 、 , 分 块 三 角 分 解 法 [4j 等 目 前 大 部 分 大 型 有 限 元 分 析 通 用 程 序 用 得较 多 的 解法 是 分 块 三 角 分 解 法 和 波前 法 上 述 一 些 解 法 虽 然 在 不 同程 度 上 都 扩 大 了 计 算 机 的 解 题 能力 大 的 限制 , 应用 但 是 它 们也 都存 在 一 些 极 , 、 对 于 波 前法 贮 器 的 许可范 围 切 的关 系 。 。 特 别 普 遍 的 是 按列 努块 的 三 角 分 解法 。 构成 了 , 受 到 最大 波 前 区 的 限 制 , 计 算 仍 旧无 法 实 现 。 如果 最 大 被 前 区 的 容 量 超 过 了 计 算 机 内 存 , 波前 区 的 大 小 与 所 求 解 的 结 构物 的 形 状 及 网格 有着 密 , 即使 是 平 面 问题 也 可 能达 到很 大 的 量 级 空 间 问 题 就更难 控 制 了 , 紧 缩 存 贮 的 分 块 的 三 角 分 解法 则受 到 最 大 半 带 宽 的 限制 的 容 量 超 过 了 计 算 机 内存 贮 器 的 容 量 计 算 也将 无法 实现 , , , 。 。 对 于 按 变带 宽 如 果 由 最 大 半带 宽 所 决 定 的 子 块 而 有 限元 空 间 问题 的 最 大 半 带 即使 在 采 取了 优 化带宽 技 术 之 后 也 难 于 期望 有 大 幅 度 的 减 小 。 总之 一 些 较 复杂 较 大 型 的有 限元 课 题 仍 旧 无 法在 中 小 型 计 算 机 上 实现 。 一 些 更 大 型 的 题 目 就 是在 带有 虚 拟 内 存 贮 器 的 大 型 计 算 机 上 也常 常 遇 到 存 贮 上 的一 些 麻 烦 。 宽 , 突 破 带 宽 的 限制 解大 型 、 对称 分 析计 算 , 、 正定 , 最 大 限度 地解 除 对 计 算 机 内存贮 容量 的 苛 求 , 稀疏 线代 数 方程 组 (集 ) 的 方 法 , 础 上 分 块 可 以 是 任意 的 理论 上 讲 , , 块 的 大 小 不 受半 带 宽 的 限制 , 。 非零 元 素 分 布 方 式 的 限 制 型 有 限 元 线 代 数方 程 组 中 , 已 经 突 破 了 带 宽的 限 制 而 不 能 求 解 的 大 型 课题 现在 可 以求 解 了 、 大 型 的有 限元 。 而 是 根据 计 算 机 的 内 存 量 来 确 定 可 适 应 非 零元 素任 意 分 布 的 情 况 。 研 究 一 种 更为 有 效 的 求 它 的 主 要 特 点是 在 按 列 分 块 的 基 块 的 大 小可 以 小 到 一 块 只 包含 系 数 矩 阵K 的一 列 元 素 , 我 们 所 期 望求 解 的 对 于 解决 日趋 复 杂 对 于 广泛 应 用 中 小 型 计 算 机和 微机 都 具 有 重要 的 意 义 本 文探 讨 的 双 列 块 法 是 一 种 新 的 分 块 的 三 角 分 解 解 法 , , 。 。 同时 实践 证 明 , , 。 它 不 受 系 数矩 阵 中 双 列 块 法 在 求解 大 这 不 仅 使 得 以前 因 为 计 算 机 容 量 不够 用 而 且 可 以 利 用 比较 普及 的 小 计 算 机 解 算 大 型 课题 , 从 。 同 时 也 减轻 了 以 往 计 算 人 员 在 编 制 有 限 元 网 格 时 为 缩 小 带 宽 或 优化 带 宽 所 付 出 的 繁 重 的 工作 。 二 、 双列 块 法 (一 ) 三 角 分 解 的 求 解 方 式 利用 方 程 组 ( 1 ) 式 中 系 数 矩 阵 K 的 对 称 正 定 性 K 二 U 7刃U 式中 U K 对 角线 元 素 为 1 的 上 三 角 队 — 县 对角阵 ‘ 则 ( 1 ) 式可 写 为 。 , 对 K 采用 按 列 分 解 的 三 角 分 解 方 式 如 下 (2 ) 第2 期 葛修 润 等 : 双 列 块 法 一 一大 型 U D U X 丁 、 稀疏 、 对 称 线 代 数方 程 组 的一 种 有 效 解 法 二 R (3 ) U X = Y D Y 二 Z U TZ = R (5 ) 过程 , 、 ( 6 ) 式 称为 前 向 回 代 过 程 两 者 合在 一 起 称 之 谓 回代 过程 (6 ) 也可 称 之 为 右端 行 约 化过 程 , , ( 4 ) 式 称 为 后 向回 代 。 ( 幻 式 系 数 矩 阵 的 分 解是 方 程 组 解 算 的 主要 部 分 。 矩 阵U 和 D 中 的 元 素 在 一 般 满 阵 分 ;_ 解 的 情 况 下 可 按下 式 求 出 ‘fj 一 一( 兰一 ) / ‘ (i 二 1 , 2 犷! 亩‘ ‘ (7 ) … …” 一 l ) , (i 二 , + 1 , 2, 李+ … …n) J 一 l J 叭 一 二 石, , 一 r 乙 ‘ 汽d 二 , , (8 ) 1 ( 二1 i 2, , .… n) · 由 于 系 数 矩 阵 K 是 按 一 维 变 带 宽 紧 缩存 贮 方式 存放 但 减 少 了 存 贮 量而 且 省 略了结 果为 零的 无 效 运 算 . 一 」 。 ’ 所 以 实际 计 算 时 」 ( r _ 、, : , r, : 。 , , , ) (7 ) 、 , , ‘ , 一 这样不 ( 8 ) 两 式可 、 ’ 改 写 成如 下 形 式 · ‘, 二 半带 宽 以 外 的 零 元素 一 律 不 存 , 一 二 、“ 影 一 丫 (9 ) (i< 厂 ) J一 l d, , 二 k ,, 一 乙 r 三” : 了 毛d r , (1 杯) - 土 岩 其 中m m ‘, 汾 别 为第 i列 和 第汀 d 的非 零元 素 的 最 小行 号 当 分解 完 后 Y 求得 U 和 D 矩 阵 , ) = ( 年 。 则 按 ( 6 ) 式可 以 求 得 向 量 z , 最 后 按 ( 4 ) 式 即得 最终 解 向量 X , 19 85 学 力 再 按 ( 5 ) 式 求 得 向量 , 。 算法 双 聆 图 所 示 为 一 个 大 带宽 的 系数矩 阵 1 。 允 为 一|l x勺 .l 习 |l 列块号 妇.1| 习 X 丫 XK X 义 减 减 X 减 K 欠 X x 务 、 火 X 伙 卜 又 火 X 丫 、 、 伙 料 曰 火 又 泛X , 、 杏{ 又 气) X 如 果 按 照通 常 的 分 块 分 解 解 法 当着 一 块 来 处 理 解 。 。 这 样 的 矩 阵形 式 由 于 受 一 个 大 带 宽 的 限制 , 其 中 的 所 有非 零 系 数 及带 宽 内零 元 素 必 须 同 时存 入 计 算 机 内 存 这 显 然 就 会 遇 到 内 存 贮量 不 够 用 的 困 难 任 意分 割 可 的 容量 譬 如图 1 上所 示 的 5 块 , 便可 进 行 求 解 具 体 的 做法 是 : 照 这 个 数组 的 大 小来 进 行 超过 一 个 列 块 数 组 的 长 度 。 。 它 只 是根据 计 算 机 许 可 的 内 存 贮 量 来 仅 仅 要 求 任 意 两 块 的 半 带 宽 内元 素 之 和 不 超 过 计 算 机 许 , , 分 别 称之 为 主 列 块数 组 和 相 关 列 块 数组 各 列 块 可 以 包 含 不 同的 列 数 列 块 按 自然顺 序 编 号 , 该 列块 的 下 列 特 征 信 息 : 始 列号 I B 、 , 1 , ‘; , 称 为 对 角元 数组 D 末 列 号 jE 、 。 。 并 立 即转 存到 计 算 机 的 外 存 贮器 贮 存 , 同 时 要记 录 所 有 列 第 一 个非 零 元 素 行 号 中 的 最 小 行 , 。 分 解 系 数矩 阵的 步 骤 概 述 如下 系 数 矩 阵 的 分 块就 按 但 各 列 块带 宽 内 的 元素 数 目 都 不 能 最 好 再 设 置 一 个 一 维 数组 存 放 系 数矩 阵分 解 的 对角 元 素 d 预 先 按各 列 块 逐 块 地 生 成 系 数 矩 阵 。 。 后 面 的 分 析将会 看 到 这样 做 的 目 的 只 是为 了 减 少 内外 存 交 换 的 次 数 号M 方 可 求 设 置 两 个 相 等 长 度 的 一 维 数 组 (它们 既 是 系数 矩 阵 生 成 的 工 作 数 组 又 是 。 另外 , 。 系 数矩 阵 分 解 的 工 作 数组 ) , 实际 上 只 能 。 双 列 块 法 对 上 述矩 阵 的 分 块 完 全 不 受 带 宽 的 限 制 , , : 将 第 1 列 块 的数 据 从 外 存 调 入 内 存 的 主 列块 数 组 。 : 葛 修润等 竿2明 2 “, 双 列J [ 法一 一 夫 型 j 将 第 1 列 块 中的 各 列 按 ( 9 ) . 3 从第 2 列 块 开 始 . , ‘, · 完 成分 解 的 第 1 列 块巷 蚌户 , 主 列 块 不 相关 ( 2) , 则表 示 该 列块 与 主 列 块 相 关 不过 , 。 , i” 1 , 并 将该 列 块 据 主 列 块数 组 不 动 , 于 是该 列 块轮 空 , 。 凡 某 列 块 内 非零元 素 的 最 小 称 之 为相关 列块 。 杏则 , 表 示与 。 , ( 3 ) 此 时 主 列 块 与 相 关 列 块并 存 分 解计 算 不过 此 时 顺 序 向后 逐 块 处 理 各 列 块 如 下 : 不 必进 入 内存 将 相 关 列块 的 数 据 从 外存诚 入 内存 的 相 关 列 块 数 组 , , 几 ‘ 行 号 M 小 于 或者等 于 IE M 种 有 效解法 , ( 1 ) 根据 主 列 块 的 末 列 号 I E M 舞断 与 其 相 关 的 列 块 号 , 一 付 称线 代 数 方 程 组 的 计 算 所 得 的 “ 存 放在 原 叭 的位 置 上 , ‘ 。 、 (l 。) 两 式 逐 列 进 行分 解 计 算 “ 各列 的 d 记 入 对 角 元 数 组D 的 相 应 位 置 上 称 之 为 主 列块 稀疏 , E M I I M 是该 列 块 的 末 列号 o E … … 、 。 按 ( 9 ) 式 对 相 关 列 块 内与 主 列 块 相关 的 元素 进 行 , 此时 (9 ) 式 中 , , i= 1 2, · 一 IE M (1 1 ) t IB R 共 i‘ IE R (1 2 ) IE 万 是 主 列 块 的 末 列 号 ; 其中 , B R 是 相 关列 块 的 始 列 号 ; 1 卫R 是 相关 列 块 的 末 列 号 。 。 ‘ 计 算 得 到 的 。 , 仍 旧 存放 在原 哥‘, 的 位 置 上 ( 4 ) 全 部 完 成相 关元 素 的 分 解 后 放该 列 块 的 地 址上 立 即将 该相 关 列 块 调 出 内 存 , 直 到最 后 一 个 相 关 列块 完 成 相 关 部 分 的 分 解并转 出 , 存入 外 存贮器 原 先存 。 ( 5 ) 逐 列 块 重复 ( 1 ) ~ 为止 . , (4 ) 。 4 . 第 一 轮循 环 到 此 结束 该 列 块 的地 址 上 此时 , , 。 主列块 , 即第 1 列块 可 以 调 出 内 存 留 待 后 向 回 代 过 龚垂娜入 使 用 , 存 入 外存 贮 器 原 先 存放 。 系 数 矩 阵 的分 解 形 势 如 图 2 中 划 斜 线 部 分 , 它 表 示 第 一 轮循 环 完 成 分 解 的 范 围 1 l } } { , ‘. 曰. . ~ 口 目 ! l ! ‘ t 曹 产 {户 { 仁 仁 七 。 土 岩 、 州 . ’ :、 、 . 氛 第典 轮 循 环 开 始 ; 力 第 2 列 块 成 为 主 列块 , ‘ 。 ( 盆 卜 该 主 列 块除 了 与 前 面 的 列 块 相 关 的 元 素 完 成 了 分 解 计 算 外 一 素 进行 分解 , 。 ( 幼 将第 名 列 块 的数 据 从 外 存 调 入 内 存 的 主 列 块数 组 。 了E M 的 部 分 包 括对 角 项 元 素 还 没 有 进 行 分 解 样 19 片5 学 刃月 ‘, 存 放 树 原来的 位 置 上 ( 3 为 重 复上 述 第 3 , 、 这 里 需着 重 补充 说 明 的 是 : 零元 素 的 最 小行 号 IB M 、 ‘ : 第 落 两步 1 0 ( ) , 。 , 、、 设, 无 需 再进 行 计 算 , 在 这 一 轮循 环 中 暂 不 作 分 解 , I : 甲 , 。 所以 , 分 解公 式 ( 9 ) 、 (1 3 ) 华护 直 到 全 部 完 成 系 数矩 阵 的 分 解 为 止 关 于 前 向何 代禅程 一 J石 R 分 别 为 参 加 而 各 列诸 元 素凡 是 其 行 号 脚 / B R 蕊声 镇 IE R ( , - 下 由此 类推 朋 「 。 IB M 百 f《 I 万M 、 。_ - 拼 ] 分 另l =为 第 i列 和 第 广列 的 非 J !甜 币也 不 需 要 运 算 一 , 同 则 参 加 运 算 的 相关 列 块 中各 列 诸 元 素 凡其 行 号 脚 标 小 于 扣 . 。 一 ‘ 6 首 先对 这 部 分 元 _ ‘ _ 。 式 可 知 i> 第 2 列 块 全 部 元 素 分解 完 毕 IE 叮 分 别为 主 列块 的 起 始 和 终 l上列 号 ; 、 。 对 第 , 块 以后 的各 列 块 中 相 关 的 元 素 进 牙 码卜解 汁算 , 都 已 在这 一 轮 循 环 以 前 分 解 完毕 标 大 于 j五 M 的 至此 , 当 主 列 块 与相 关列 块 并 存 时 运算 的 根关列 块 的起 始 和 终 止死号 ]B M 的 。 “ 块 内 的 d 记 入 对 角 元数 组 D 中 , 一 , 如 图 2 中 画 竖 线 的 部分 所 示 这 些 分 解 计 算 只 与 本块 内元 素有 关 , ) 从 l ( l , ‘ 鱿 。 一 ’ 、 一 般 表达 式 如 下 i一 】 z 一 R ‘一 ‘ y . 1 5 ) 上述 ( 置中 。 兰 : , ‘ /d 乙 2 。r 1 (15 ) 。‘ (16) ‘ 式 的 计 算是 在 各 列块 的 系 数分 解过 程 中 同 时 完 成 盯 (1 6 ) 式 是 在 分 解 过 程 全 部 完 成 后 进 行 的 元 数 组D 中 换 的 次数 , ‘ 所 以 在计 算 ” 时 。 , 不 必 逐个 列 块 从 外 芭 , z , 就存 放 在 原 先 存放 R ‘ 的 位 由 于 对角 元 素 d 亨中 调 入 数 据 了 , ‘ , 预 先存 放 在专 设 的 对 角 从 而 省 略 了 许 多 内外 交 (四 ) 关 于 后 向 回 代 过 程 一 般 表 达 式 如下 义, = , ‘一 u ‘r x 艺 r 二 豆十 r (1 7 ) 1 ( 了= n , 刀 一 1 , … … 1) 葛修 润 等 第2 期 : 、 , 双 列 块 法 一一 大 型 、 稀 嘛 对称 线代 数 方程组 的一 种 有 效 解法 , 当采 用 按 列 分 解 的 双 列 法 时 行的 不 能直接 套 用 上 式 按 行运 算的 格 式‘ 底 向回 代过程也 是 按 列 进 从 调 入 最后 月 个 列 垅 从 最 后 一 歼 开 始 丫 逆 序 进 行 , 对 于 最 后 一列 , 头 即 是x 。 万 井 由 此 得 到x ‘ (i < 的 。 。 - · - , · 一 _ · : 一 . 一、 , 一 一 : 、 、 产 0 1 1( 8 1 , r 了 厂 。 “ 夕 的 第一 次 近 似 值 州 一 , ‘ 公 ,尸 一 “ 叫卜 价 矿汽 飞 草瓜 当进 行 到 第 , 列 时 笼 x f Zo 二 X ” 一 ’十 乒 ’) = x 一 ” 一 u ‘, x J 乒 (i 1 = , 2, , (当 i< 。 , 时 , (2 1 少 · 理 ) + 皿) ’ ” . , 了二 0 ) , 、 肠 当 调 入 最 后 一 个 列块 = 1时 进 行 到了 , : · 方 程 组 的 全 部 解 即 已获 得 云 ” ’ 尸 . 讨 口 .了 吧 J j 一 , - 介卜 , 狱 二 , 声 卜 勺 才少 、 、 三 算 例与讨 论 应 用 上 述 双 列 块 法对 某 三 维 问 题 进行 了 有 限 元 分 析 计 算 个 20 节 点 的 等 参元 。 这 个 间题 的 有 限元 网格 由 1 2 4 个 16 节 点 的 等参 节 理 元 、 刚 度 矩 阵 K 在 上 三 角带 宽 内的元 素 总 长 为 1 2 4 6 , 536 , 。 而 我 们应 用 双 列 块 法 在 中 国 科 学 院 武汉 分 院 8 、 , 计 算 机 的 内 存 贮 容 量 为 5 兆 字 节 以上 方 可 求 解 共 83 1 个 节 点组 成 。 其 最 大 半 带宽 为 1 74 6 该 矩 阵 按 一 维 变带 宽 紧缩 存 贮 方 式需 要 计 算 站 的 小型 计 算 机 PE 3 2 2 0 上 仅 用 0 6 8 5 兆字节 的 内 存容 量 就 求 解 成 功 . 一 1 块 求解 上 述 算 例 说 明 双 列 块 法 可 以在 较 小 的 内存 情 况 下 进 行 大 型 有 限元 线 代 数方程组 的分 。 摆 脱 了 最 大 带宽 的 限 制 . 。 总之 , , 从 而 适 应 非 零元 素任 意 分 布 的 情 况 突 破 带 宽 的 限 制是 一 个 很 重 要 的 问题 在 双 列块 法运 行 中 的 相关 列 与 不 相 关 列 , , 单元 。 . , 每 一 相 关 列 内的 相 关 元 素与 不 相 关 元 素 在 双 列 块法 的 程 序 设 计中 这 些 单元 占内 存很 少 对 提高 运 行效 率是 必 要 的 。 , , , 因而 具有 较 大 的 优 越 在这 里 得 到 了 解 决 可 以 灵 活 地 判 别 相 关 列 块 与不 相 关 列 块 这 样 做 减 少 了许 多 不 必 要 的 内外 交 换 和 一 些 不 必 要 的 运 算 3 。 . 性和通 用 性 2 , , , 。 以及 每 一 相 关 列 块 内 有效 运 算与 无 效运 算等 等 从 而 提 高 了 运 行 的 效率 。 。 设 置 了 对 角 元 数 组 D 和 存放 各 列 块 一 些 特 征 信 息 的 存 贮 而 且 有 些 信 息 可 以随 列 块 数据 同时 贮 存 在外 存 贮 器 内 。 这样做 岩 . 4 双 列 块法 由于 它是 按 列 分 解 计 算 。 所 以它 可 以适应 各 种 类 型 的 计 算 机 办 土 但是 1 自5 5 年 学 , 内 存 的 节 省 是 靠 外 存 贮器 来 弥 补 的 。 次数 双 列 块 法 对 系 数 矩 阵 的 分 块 是 根 据 计 算 机 所 许 可 的 丙 存 贮 量来 决 定 的 所 以一 般 情 况 下 次 数 降到 最 低 限 度 . 6 , 一 般 具 有带 状 对 称 系 数矩 阵 的 线 代 数方 程组 。 , 〔1 〕 H in t o n E 〔2 〕 s c h r e m , E . an d . , c o m p u te r W II o n s , E 李 大潜等 L . E q u a ti o n s , o w en e o M t h ds C o m Pu t e r ”J 。 块 的 大小 从 不 过 这 样 就 会有 大 量 的 内外 交 换 的 使 分 块数 尽 量 少 一 些 , , 把 刀0 。 按 三 角分 解方 法 求 解 , ” 代 表 矩 阵 的平 均 , 其中 代表 矩 阵 的 阶数 , , 所需 的 运 算 次 。 参 ” j 任 、l b JJI 5 。 应 该 尽 量 利 用 计 算 机所 许 可 的 容 量 数是 按 耐/ 2 来 估 算 的 这 一 点也 适 用 于 双 列 块 法 忆 Ž 尹 厂 ,‘ 沙” r 七 n J 这方 面 , 。 n 半带 宽 故 计算机需 , 根 据 目前 计 算 机 的 发 展 情 况 理 论 上 讲 可 以小 到每 个 子 块 只 包 含 系 数矩 阵 的一 列 元 素 。 , . , B a th e n I te r . . D , J C . J S u rv e y 〔7 〕 玛 康 二 数 值计算 方 法 , F in it E le m e n t P r o g r a m m in g , . J . D o h e r ty 一 w , m p u to r 袁 建新 王可钧 杨家岭 一 献 o F ih i t e f th e , 、 IA I N s D u ff A . 文 s t r u c t u r a l M e e h a n ic s 1 9 7 1 K o . 考 I m p le m e n t a t 主 石n in , R 有 限元 素法 续讲 、 . , 。 完 全 可 以 满 足 算题 的 需 要 . 分 块 不 受 计算 机 内存贮 容量 的 限制 按列 分块 带 有 较 丰 富 的 外 存 贮 设 备 并 具 备 一 定 的 内外 交 换 速 度 5 一 , , , and s r M 自t ix 国 防 工 业 出版社 , 年 。 , . N u m o r ic a i a n j o f La rg e S y st em s o f L in e ar 19 7 奋 · 。 Pr 二 R 19 78 , 静力程 序 一含节理 的 f s p a r se E le m e n t p r o e e d u r e S o lu t io n V OI 4 . 科 学 出版 社 1 9 7 7 年 一 o S t ru e t u , , 。 一 D ire c t p 一 , G JP 1 , . A e a d e m ie p r e s s 1 9 7 7 . o e . o , 岩 土 力学 f th e iE , 邵 v , 1 98 3 年第 1 期 o l. 6 5 , No . 4 , 。 10 77 . 葛修 润 等 第召期 : 双 列 块 法一 一 大型 T h e D o u b le C o lu m n fo r L a r g e 、 3弓 稀疏 对称 线 代数方 程组 的一 种 有效解法 M e th o d B lo e k sy m s Pa r s e 、 a n , m e t r ie S y s t e m L in e a r E q u a t i o n s o f Jia lin g Y ang G e X iu r u n S o lu t io n E ffe e t i v e A b s tr a e t 一 T h e d o u b le C o lu m n b lo e 戈 m e t h o d a pp lie s to n e 。u e a n 。 n 。 e e l m e n t 、n 。厅5 15 ‘ 宕 和 t so , 、 五 it 猛枷 、 ‘ u s d e f t 。 t p ’ A r e; eh t fo i - 。o 。 。。 毛ffi i a l 五 w it h z v in g e it h en ee “ i a l f P c s y th 1 : “ an d w id th “ t加 e · i fo r t s hi d 俪 。拓 e , p le te ly in d e p e n d e n t fie ie n t m a tr ix 15 p r o v e d t he 12 4 tw e n ty n o d e an o 一 a m a x im u m f m o r e th a n eo m p u te r an d 5000 o n ly ie te d 毗 l a i r o 。n ‘ eo pr o 讹比o m a e eo r 13 v e 抓。o e o 一 一 b y te s . l - · T he sto r a g e eo o be ap p lie d to e a le u la tio n s in , p a r t iti。 n e te r eo r e e ‘s e a l F E p 拍从 m eo m 训 e l 馆 a 二 b 沙m e a n s th e e o e f 174 6 s to r a g e 一 e 派 厂 久 一 ; s m an f bu m 吐h 。 d th e r s to r a g e e o r e ffe e tiv e B a se d . 一 an e le m e n t s s b y te s w a s la r g e s e a le F E an u se d . ’ , c o e e a Pa e f: it y lt . m e th o d o n th i s FE P r o b le m w ith d 53 1 de s a n d g lo b a l s tiffn e s s m a t r ix w a s p e r fo r m e d 已 s一 一 一 饯 r e e d im e n s io n a l m p u t a tio n f 685 K o m Pu te r is o p a r a m e tr ie 一 w it h th . o 。 b y t h 。 d 。。lb e 的l奴m 仓 b 麦 石e k m t五 d e o m p u te r b lo e k m e th o d m a k e s i t p o s s i b le fo r m in 乒 to m g e n e r a lly t五。 5 0 2。, i。 。 。 f p r o b lo , - - ’ f th e h a lf b a n d w id th e o re so fu l a n d de a 们 to s u e e 万s s n o i th e to s。 lin e a r sp ar se o e th o d i , in F E i n g d in g t o te e n s x 。q u a t o n s it 。 b a o d w id t h b l恤 o K o t ho d m p le t e d d 5 . f la 馆 e o d e e o m p o s it io n e 。r li五 of f t h e b a n d w sd th th a t t h is 及 p p r o a e h be en h a v in g 。 15 p a r t itio n e d lu t io n h a s so m s r e s tr , T h is d iffie u lty h 。。 b o e o eo m an g u a r tr 宜 l d e p e n d en t m a tr i x d iffie u lt 5 : y st e la r g e e n t b a rg e p a r ti tio n e d rh e lu te s o . o n n o , , sto r a g e PE 3 2 2 0 一 T h e d o u b le m in i e o lu m n d h ig h le v e l m ie r o e o m p u te r p r o b le m 一 s. -