物联网工程专业庞艳杰—电子技术基础.pdf

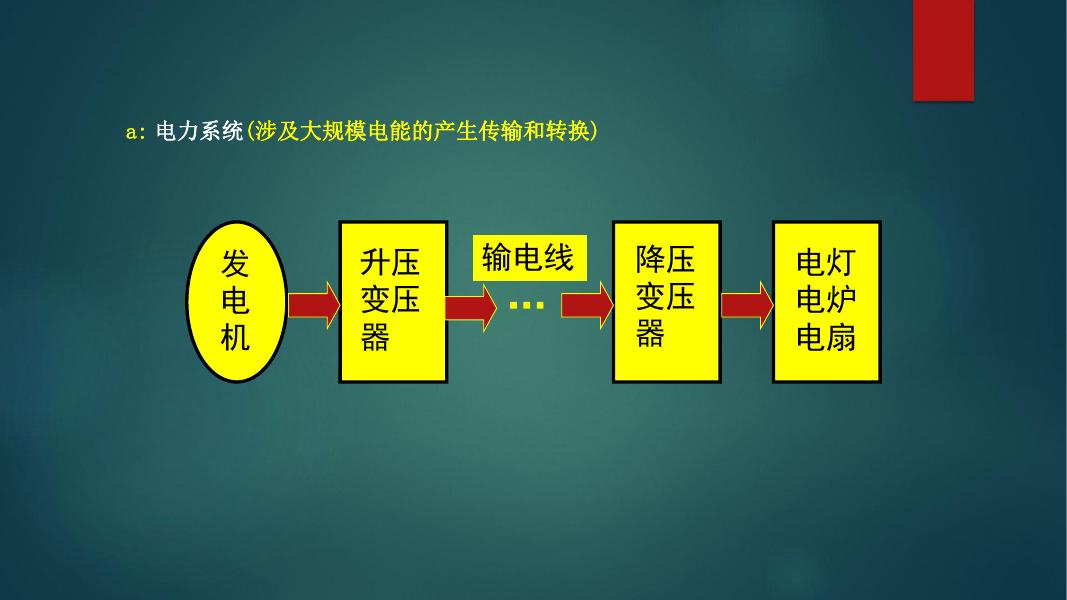
电子技术基础 信息工程学院 庞艳杰 第1章 电路模型和电路定律 本章重点 1.1 电路和电路模型 1.5 电阻元件 1.2 电流和电压的参考方向 1.6 电压源和电流源 1.3 电功率和能量 1.7 受控电源 1.4 电路元件 1.8 基尔霍夫定律 首页 l 重点： 1. 电压、电流的参考方向 2. 电阻元件和电源元件的特性 3. 基尔霍夫定律 1.1 电路和电路模型 1.实际电路 由电工设备和电气器件按预期 目的连接构成的电流的通路。 功能 a 能量的传输、分配与转换； b 信息的传递、控制与处理。 共性 建立在同一电路理论基础上。 a: 电力系统(涉及大规模电能的产生传输和转换) 发 电 机 升压 变压 器 输电线 降压 变压 器 电灯 电炉 电扇 b:扩音机(信息的传递、控制与处理) 话筒 扬声器 放 大 器  电路组成： (1)电源或信号源：发电机、电池。供应电能设备。 (2)负载：如灯泡、扬声器。取用电能的设备。 (3)中间环节：导线、开关、变压器、放大器等。 2. 电路模型 电路图 开关 te la p ll a w -T E S A B 0 1 灯泡 电池 Rs RL Us 导线 l电路模型 l理想电路元件 反映实际电路部件的主要电磁 性质的理想电路元件及其组合。 有某种确定的电磁性能的理想 元件。 5种基本的理想电路元件： 电阻元件：表示消耗电能的元件 电感元件：表示产生磁场，储存磁场能量的元件 电容元件：表示产生电场，储存电场能量的元件 电压源和电流源：表示将其它形式的能量转变成 电能的元件。 注意 ①5种基本理想电路元件有三个特征： （a）只有两个端子； （b）可以用电压或电流按数学方式描述； （c）不能被分解为其他元件。 注意 ①具有相同的主要电磁性能的实际电路部件， 在 一定条件下可用同一电路模型表示； ②同一实际电路部件在不同的应用条件下，其电路 模型可以有不同的形式。 例 电感线圈的电路模型 1.2 电流和电压的参考方向 电路中的主要物理量有电压、电流、电荷、磁 链、能量、电功率等。在线性电路分析中人们主要 关心的物理量是电流、电压和功率。 1.电流的参考方向 l电流 带电粒子有规则的定向运动 l电流强度 单位时间内通过导体横截面的电荷量 A（安培）、 kA、mA、A l单位 l方向 1kA=103A 1mA=10-3A 1  A=10-6A 规定正电荷的运动方向为电流的实际方向 元件(导线)中电流流动的实际方向只有两种可能: 实际方向 A A   B 实际方向 B 问题 对于复杂电路或电路中的电流随时间变化 时，电流的实际方向往往很难事先判断。 l参考方向 i A 任意假定一个正电荷运动的方 向即为电流的参考方向。 表明 电流(代数量) 参考方向 B 大小 方向(正负） 电流的参考方向与实际方向的关系： i A i 参考方向 实际方向 i>0 B A 参考方向 实际方向 i<0 B 电流参考方向的两种表示：  用箭头表示：箭头的指向为电流的参考方向。 A i 参考方向 B  用双下标表示：如 iAB , 电流的参考方向由A指向B。 A iAB B 2.电压的参考方向 l 电位 单位正电荷q 从电路中一点移至参考 点（＝0）时电场力做功的大小。 单位正电荷q 从电路中一点移至另 一点时电场力做功（W）的大小。 l 电压U l 实际电压方向 l 单位 电位真正降低的方向。 V (伏)、kV、mV、V a 例 b 已知：4C正电荷由a点均匀移动至b点电场力做功8J， 由b点移动到c点电场力做功为12J， ① 若以b点为参考点，求a、b、c点的电位和电压 U c 解 (1) b  0 U ab   a  b  2  0  2 V Wab 8 a   2V q 4 U bc  b  c  0  (3)  3 V Wcb Wbc 12 c      3 V q q 4 解 a (2) c  0 b Wac 8  12 a   5V q 4 Wbc 12 b   3V q 4 U ab   a  b  5  3  2 V c 结论 U bc  b  c  3  0  3 V 电路中电位参考点可任意选择；参考点 一经选定，电路中各点的电位值就唯一确定；当 选择不同的电位参考点时，电路中各点电位值将 改变，但任意两点间电压保持不变。 问题 复杂电路或交变电路中，两点间电压的实 际方向往往不易判别，给实际电路问题的 分析计算带来困难。 l 电压(降)的参考方向 + + 参考方向 U 实际方向 U >0 假设高电位指向低电 位的方向。 参考方向 U – – + – – 实际方向 U<0 + 电压参考方向的三种表示方式： (1) 用箭头表示： U (2)用正负极性表示 + (3)用双下标表示 A U UAB B 3.关联参考方向 元件或支路的u，i 采用相同的参考方向称之为 关联参考方向。反之，称为非关联参考方向。 i i + u 关联参考方向 - - u 非关联参考方向 + 例 ＋ A u － i B 电压电流参考方向如图中所标， 问：对A、B两部分电路电压电 流参考方向关联否？ 答：A电压、电流参考方向非关联； B电压、电流参考方向关联。 注意 ① 分析电路前必须选定电压和电流的参考方向 ② 参考方向一经选定，必须在图中相应位置标注 (包括方向和符号)，在计算过程中不得任意改变 ③参考方向不同时，其表达式相差一负号，但电压、 电流的实际方向不变。 1.3 电功率和能量 1.电功率 dw p dt 单位时间内电场力所做的功。 dw u dq dq i dt dw dw dq p   ui dt dq dt 功率的单位：W (瓦) (Watt，瓦特) 能量的单位：J (焦) (Joule，焦耳) 2. 电路吸收或发出功率的判断 l u, i 取关联参考方向 + u i u i + P=ui 表示元件吸收的功率 P>0 吸收正功率 (实际吸收) P<0 吸收负功率 (实际发出) l u, i 取非关联参考方向 P = ui 表示元件发出的功率 P>0 发出正功率 (实际发出) P<0 发出负功率 (实际吸收) 例 + I1 U1 － + 1 U6 － 6 － + U5 5 － I3 + U4 4 2 U2 － + U3 3 + I2 求图示电路中各 方框所代表的元件吸 收或产生的功率。 － 已知： U1=1V, U2= -3V，U3=8V, U4= -4V, U5=7V, U6= -3V，I1=2A, I2=1A,，I3= -1A + I1 U1 － + 1 U6 － 6 － + U5 5 － I3 + U4 4 2 U2 － + U3 3 + － 注意 I2 解 P1  U1I1  1 2  2W（发出） P2  U 2 I1  (3)  2  6W（吸收） P3  U 3 I1  8  2  16 W（吸收） P4  U 4 I 2  (4) 1  4 W（吸收） P5  U 5 I 3  7  (1)  7 W（吸收） P6  U 6 I 3  (3)  (1)  3W（吸收） 对一完整的电路，满足：发出的功率＝吸收的功率 1.4 电路元件 1. 电路元件 是电路中最基本的组成单元。 5种基本的理想电路元件： 电阻元件：表示消耗电能的元件 电感元件：表示产生磁场，储存磁场能量的元件 电容元件：表示产生电场，储存电场能量的元件 电压源和电流源：表示将其它形式的能量转变成 电能的元件。 注意 如果表征元件端子特性的数学关 系式是线性关系，该元件称为线性元件，否 则称为非线性元件。 1.5 电阻元件 1.定义 电阻元件 f (u , i )  0 对电流呈现阻力的元件。其特性可 用u～i平面上的一条曲线来描述： u 伏安 特性 i 0 2.线性时不变电阻元件 任何时刻端电压与电流成正比的电阻元件。 R l 电路符号 l u～i 关系 满足欧姆定律 u u  Ri Ru i i  u R  Gu u、i 取关联 参考方向 i + l 单位 i 0 R u 伏安特 性为一 条过原 点的直 线 － R 称为电阻，单位： (Ohm) G 称为电导，单位：S (Siemens) 注意 欧姆定律 ①只适用于线性电阻( R 为常数）； ②如电阻上的电压与电流参考方向非关 联，公式中应冠以负号； ③说明线性电阻是无记忆、双向性的元 件。 i R 则欧姆定律写为 u u  –R i + i  –G u 公式和参考方向必须配套使用！ 3.功率和能量 l 功率 i + u i - R - R u p  u i i2R u2 / R p  u i (–R i) i + –i2 R  - u2/ R 表明 电阻元件在任何时刻总是消耗功率的。 从 t0 到 t 电阻消耗的能量： l 能量 t t 0 0 WR  t pdξ  t uidξ u 4.电阻的开路与短路 l 开路 ++ uu –– i i R i0 u0 R   or G  0 u l 短路 i0 u0 R  0 or G   i 0 0 i 1.6 电压源和电流源 1.理想电压源 l定义 其两端电压总能保持定值或一定 的时间函数，其值与流过它的电 流 i 无关的元件叫理想电压源。 i l电路符号 + uS _ l理想电压源的电压、电流关系 ①电源两端电压由电源本身决定，与外电路无关； u 与流经它的电流方向、大小无关。 ②通过电压源的电流由电源及 uS 外电路共同决定。 例 i + uS R - 外电路 uS i 0 R i  0 ( R  ) i   ( R  0) 电压源不能短路！ i 直流电压源 的伏安关系 P  uS i l电压源的功率 i + _ + uS ①电压、电流参考方向非关联； 物理意义： u 外力克服电场力作功，电源发出功率 _ i + _ 发出功率，起电源作用 + uS P  uS i ②电压、电流参考方向关联； u 物理意义：电场力做功，电源吸收功率 _ P  uS i 吸收功率，充当负载 解 uR  (10  5)  5V uR 5 i    1A R 5 R  5Ω _ uR + 5V - P10V  uS i  10  1  10W 发出 P5V  uS i  5  1  5W 吸收 PR  Ri  5  1  5W 2 满足：P（发）＝P（吸） + + 例 计算图示电路各元件的功率 吸收 i _ 10V 2.理想电流源 l 定义 l 电路符号 其输出电流总能保持定值或一定的 时间函数，其值与它的两端电压u 无关的元件叫理想电流源。 iS + u _ l 理想电流源的电压、电流关系 ①电流源的输出电流由电源本身决定，与外电路无 关；与它两端电压方向、大小无关。 返 回 上 页 下 页 u ②电流源两端的电压由电源及外电路共 同决定。 直流电流源的 伏安关系 例 + u  RiS iS R u 外电路 0 u  0 ( R  0) u   ( R  ) 电流源不能开路！ iS i 实际电流源的产生： 可由稳流电子设备产生，如晶体管的集电极 电流与负载无关；光电池在一定光线照射下光电 子被激发产生一定值的电流等。 l 电流源的功率 P  uiS ①电压、电流的参考方向非关联； P  uiS 发出功率，起电源作用 ②电压、电流的参考方向关联； P  uiS 吸收功率，充当负载 解 计算图示电路各元件的功率 i  i S  2 A + i 5V u u  5V - P2 A  iS u  2  5  10 W 发出 P5V  uS i  5  (2)  10W 发出 满足：P（发）＝P（吸） + 例 _ 2A 实际电源 1. 干电池和钮扣电池（化学电源） 干电池电动势1.5V，仅取决于（糊状）化学材料，其大 小决定储存的能量，化学反应不可逆。 钮扣电池电动势1.35V，用固体化学材料，化学反应不可逆。 干电池 钮扣电池 2. 燃料电池（化学电源） 电池电动势1.23V。以氢、氧作为燃料。约40-45%的化学能 转变为电能。实验阶段加燃料可继续工作。 氢氧燃料电池示意图 3. 太阳能电池（光能电源） 一块太阳能电池电动势0.6V。太阳光照射到P-N结上， 形成一个从N区流向P区的电流。约 11%的光能转变为电 能，故常用太阳能电池板。 一个50cm2太阳能电池的电动势0.6V,电流0.1A 太阳能电池示意图 太阳能电池板 4. 蓄电池（化学电源） 电池电动势2V。使用时，电池放电，当电解液浓度小 于一定值时，电动势低于2V，常要充电，化学反应可逆。 蓄电池示意图 1.7 受控电源(非独立源) 1.定义 电压或电流的大小和方向不是给定 的时间函数，而是受电路中某个地方的电压(或电 流)控制的电源，称受控源。 l 电路符号 + – 受控电压源 受控电流源 2.分类 根据控制量和被控制量是电压u 或电流i，受控源 可分四种类型：当被控制量是电压时，用受控电压 源表示；当被控制量是电流时，用受控电流源表示。 ①电流控制的电流源 ( CCCS ) i1 i2 四端元件 + + i2   i1 u2 u1  : 电流放大倍数  i1 _ _ 输入：控制部分 输出：受控部分 ②电压控制的电流源 ( VCCS ) i1 i2 i2  gu1 + + g: 转移电导 u u1 2 gu1 _ _ ③电压控制的电压源 ( VCVS ) i1 i2 + u1 _ + _  u1 + u2 _ u2   u1 : 电压放大倍数 ④电流控制的电压源 ( CCVS ) i1 i2 u2  ri1 + + + ri1 u2 r : 转移电阻 u1 _ _ _ ic   ib 例 ib ic ic i b ib 电路模型 3.受控源与独立源的比较 ①独立源电压(或电流)由电源本身决定，与电 路中其它电压、电流无关，而受控源电压(或 电流)由控制量决定。 ②独立源在电路中起“激励”作用，在电路中产 生电压、电流，而受控源是反映电路中某处的 电压或电流对另一处的电压或电流的控制关系， 在电路中不能作为“激励”。 例 求：电压u2 解 i1  6  2 A 3 u2  5i1  6  10  6  4V + u1=6V i1 _ + 5i1 3 + u2 _ 1.8 基尔霍夫定律 基尔霍夫定律包括基尔霍夫电流定律 （KCL）和基尔霍夫电压定律( KVL )。它反 映了电路中所有支路电压和电流所遵循的基 本规律，是分析集总参数电路的基本定律。 基尔霍夫定律与元件特性构成了电路分析的 基础。 1.几个名词 ①支路 电路中通过同一电流的分支。 i1 + + uS1 _ uS2 R1 R2 ②结点 _ b b=3 i3 a i2 R3 三条以上支路的连接点称为 结点。 n=2 两结点间的一条通路。由支路 构成 由支路组成的闭合路径。 l=3 ③路径 ④回路 + uS1 _ R1 uS2 1 3 + _ 2 R3 R2 对平面电路，其内部不含任 何支路的回路称网孔。 注意 网孔是回路，但回路不一定是网孔。 ⑤网孔 2.基尔霍夫电流定律 (KCL) 在集总参数电路中，任意时刻，对任意结点流 出（或流入）该结点电流的代数和等于零。 流进 的电 m 流等 or i入＝ i出 i (t )  0  b 1 于流 出的 令流出为“+”，有： i5 电流  例 i1 i4 i3 i2   i1  i 2  i3  i 4  i5  0 i1  i 2  i3  i 4  i5 返 回 上 页 下 页 例 i1  i4  i6  0  i2  i4  i5  0 i3  i5  i6  0 三式相加得： i1  i2  i3  0 i1 1 i4 i2 2 i3 i6 i5 3 表明 KCL可推广应用于电路中包围多个结点 的任一闭合面。 明确 ①KCL是电荷守恒和电流连续性原理在电路中 任意结点处的反映； ②KCL是对结点处支路电流加的约束，与支路 上接的是什么元件无关，与电路是线性还是 非线性无关； ③KCL方程是按电流参考方向列写的，与电 流实际方向无关。 3.基尔霍夫电压定律 (KVL) 在集总参数电路中，任一时刻，沿任一回路，所 有支路电压的代数和恒等于零。 m  u (t )  0 or  u降＝ u升 b 1 U2 ①标定各元件电压参 考方向 + US1 _ I1 ②选定回路绕行方向， 顺时针或逆时针. U1 R1 I2 R2 _ I3 R3 I4 R4 US4 + U4 U3 U2 + US1 _ I1 U1 R1 I2 R2 _ I3 R3 I4 R4 US4 + U3 U4 –U1–US1+U2+U3+U4+US4= 0 或： U2+U3+U4+US4=U1+US1 –R1I1+R2I2–R3I3+R4I4=US1–US4 注意 KVL也适用于电路中任一假想的回路。 例 Us _ U2 + - U1 + + _ a U ba  U1  U 2  U S b 明确 ①KVL的实质反映了电路遵从能量守恒定律; ②KVL是对回路中的支路电压加的约束，与回路 各支路上接的是什么元件无关，与电路是线性 还是非线性无关； ③KVL方程是按电压参考方向列写，与电压实际 方向无关。 4. KCL、KVL小结： ① KCL是对支路电流的线性约束，KVL是对回 路电压的线性约束。 ② KCL、KVL与组成支路的元件性质及参数无关。 ③ KCL表明在每一节点上电荷是守恒的；KVL是 能量守恒的具体体现(电压与路径无关)。 ④ KCL、KVL只适用于集总参数的电路。 思考 ？ I=0 1. 1 2. + 3V _ i2 1 1 1 A B 1 + 2V 1 _ i1 ? UA =UB ? i1=i2 例1 求电流 i 3A  2A 3Ω 3Ω 5Ω 例2 1Ω i?  20V  4Ω 求电压 u  10V  u  ?  5V  解 解 i  3  ( 2 )  5 A u  10  20  5  15V 例3 求电流 i i =? + 3 解 - 4V + 5V 3i  4  5  i  3A 解 例4 求电压 u + 1A + u =? u  5  7  12V 要求 - 3 - 4V + 5V - 能熟练求解含源支路 的电压和电流。 例5 求电流 I I1 10 + 10V 解 1A 解 I =? + -10V - I  10  3  7 A 4  U  2I  0 U  2 I  4  14  4  10V 10 I1  10  (10)  0 I1  2A I  I1  1  2  1  3A 例6 求电压 U + 10A 4V + 2 U =? I - 3A 5 - + 5 - 10 I2   1A 55 5 + - 解 I =0 I2 + 10V 3I2 + 例7 求开路电压 U U=? - 2I2 U  3I 2  5I 2  5  2 I 2  2 I 2  2V 例8 求输出电压 U + US - I1 R1 I1 解 + R2 U=? －  R2U S U  R1 (1   ) U   R2 I1 I1   I1  U S R1 US I1  R1 (1   ) 第2章 电路的一般分析方法和电 路定理 5A 2A 3 4 I＝？ 问题引入 7 5 15 6 a b 20 7 6 2.1 电阻电路的等效变换 本节重点 1 引言 2 电路的等效变换 3 电阻的串联和并联 4 电压源、电流源的串联和并联 5 实际电源的两种模型及其等效变换 6 输入电阻 l 重点： 1. 电路等效的概念； 2. 电阻的串、并联； 3. 电压源和电流源的等效变换； 1 引言 l电阻电路 仅由电源和线性电阻构成的电路 l分析方法 ①欧姆定律和基尔霍夫定律是 分析电阻电路的依据； ②等效变换的方法,也称化简的 方法。 2 电路的等效变换 1.两端电路（网络） 任何一个复杂的电路, 向外引出两个端钮，且 从一个端子流入的电流等于从另一端子流出的电流， 则称这一电路为二端网络 (或一端口网络)。 i i 无 源 无 源 一 端 口 2.两端电路等效的概念 两个两端电路，端口具有相同的电压、电流 关系,则称它们是等效的电路。 B i + u - 等效 C i + u - 对A电路中的电流、电压和功率而言，满足： B A C A 明确 ①电路等效变换的条件： 两电路具有相同的VCR； ②电路等效变换的对象： 未变化的外电路A中的电压、电流和功率； （即对外等效，对内不等效） ③电路等效变换的目的： 化简电路，方便计算。 3 电阻的串联和并联 1.电阻串联 R1 Rk + u1 _ + u ①电路特点 i + Rn k _ + un u _ _ (a) 各电阻顺序连接，流过同一电流 (KCL)； (b) 总电压等于各串联电阻的电压之和 (KVL)。 u  u1      uk      un ②等效电阻 Rk + u1 _ + u + u 由欧姆定律 Rn k _ + un Re q _ 等效 i _ + i R1 u _ u  R1i    RK i    Rni  ( R1    Rn )i  Reqi n Req  R1    Rk    Rn   Rk  Rk k 1 结论 串联电路的总电阻等于各分电阻之和。 ③串联电阻的分压 u Rk uk  Rk i  Rk  uu Req Req 表明 电压与电阻成正比，因此串联电阻电路 可作分压电路。 例 两个电阻的分压： R1 R2 u1  u u2  u R1  R2 R1  R2 i + u+ 1 u + u2 _ º R1 R2 ④功率 p1=R1i2， p2=R2i2，， pn=Rni2 p1: p2 :  : pn= R1 : R2 :  :Rn 总功率 p=Reqi2 = (R1+ R2+ …+Rn ) i2 =R1i2+R2i2+ +Rni2 表明 =p1+ p2++ pn ①电阻串联时，各电阻消耗的功率与电阻大小 成正比； ②等效电阻消耗的功率等于各串联电阻消耗功 率的总和。 2. 电阻并联 ①电路特点 i + u _ R1 i1 R2 i2 Rk ik Rn in (a)各电阻两端为同一电压（KVL)； (b)总电流等于流过各并联电阻的电流之和(KCL)。 i = i1+ i2+ …+ ik+ …+in ②等效电阻 i + i1 i2 R R R 1 2 k u i ik Rn in 等效 _ 由KCL: + u _ i = i1+ i2+ …+ ik+ …+in =u/R1 +u/R2 + …+u/Rn =u(1/R1+1/R2+…+1/Rn)=uGeq n Geq  G1  G2    Gn   Gk  Gk k 1 Req 结论 等效电导等于并联的各电导之和。 1 1 1 1  Geq      Req R1 R2 Rn 电流分配与 电导成正比 ③并联电阻的分流 ik u / Rk Gk   i u / Req Geq 即 Req  Rk Gk ik  i Geq 例 两电阻的分流： 1 R1  1 R2 R1 R2 Req   1 R1  1 R2 R1  R2 i R1 1 R1 R2i i1  i 1 R1  1 R2 R1  R2 1 R2 R1i i2  i  (i  i1 ) 1 R1  1 R2 R1  R2 i1 R2 i2 p1=G1u2， p2=G2u2，， pn=Gnu2 ④功率 p1: p2 :  : pn= G1 : G2 :  :Gn 总功率 p=Gequ2 = (G1+ G2+ …+Gn ) u2 =G1u2+G2u2+ +Gnu2 =p1+ p2++ pn 表明 ①电阻并联时，各电阻消耗的功率与电阻 大小成反比； ②等效电阻消耗的功率等于各并联电阻消 耗功率的总和 3.电阻的串并联 电路中有电阻的串联，又有电阻的并联，这种 连接方式称电阻的串并联。 例1 计算图示电路中各支路的电压和电流 i1 5 i1 5 i2 i3 6 165V 18 i5 4 i4 12 + + i1  165 11  15A i2 i3 165V 18 6 9 - u2  6i1  6  15  90V i1 5 i2 i3 6 165V 18 i5 4 i4 12 + i2  90 18  5A u3  6i3  6  10  60V i3  15  5  10A u4  3i3  30V i4  30 4  7.5A i5  10  7.5  2.5A I1 例2 + 12V 解 _ I2 R I3 R + + 2R U1 2R U2 2R _ _ I4 求：I1 ,I4 ,U4 + 2R U4 _ ①用分流方法做 I 4   1 I 3   1 I 2   1 I1   1 12   3 2 4 8 8 R 2R U 4   I 4  2 R  3V I1  12 R ②用分压方法做 U2 1 U4   U1  3V 2 4 3 I4   2R 从以上例题可得求解串、并联电路的一般步骤： ①求出等效电阻或等效电导； ②应用欧姆定律求出总电压或总电流； ③应用欧姆定律或分压、分流公式求各电阻上的电 流和电压。 以上的关键在于识别各电阻的串联、并联关系！ c 例3 a 6 15 b d 5 5 求: Rab , Rcd Rab  (5  5) // 15  6  12Ω Rcd  (15  5) // 5  4Ω 注意 等效电阻针对端口而言 Rab＝70 例4 求: Rab a b 20 100 10 40 60 80 a 20 50 a b 20 100 100 60 120 a b 100 b 20 40 100 60 60 20 例5 求: Rab 5 15 5 a b 20 6 15 缩短无 电阻支路 7 a b 7 6 6 6 4 4 Rab＝10 15 10 a b 15 3 a b 7 例6 求: Rab c 对称电路 c、d等电位 R R R 断路 短路 i i a a i b i 2 R 1 R R d 1 根据电流分配 i1  i  i2 2 1 1 uab  i1 R  i2 R  ( i  i ) R  iR 2 2 uab Rab  R i c R b R d Rab  R 4 电压源、电流源的串联和并联 1.理想电压源的串联和并联 注意参考方向  usk ①串联 u  u s1  u s 2  uS1 uS2 _ _ + + 等效电路 _ + u ②并联 + u 等效电路 u  u s1  u s 2 注意 相同电压源才能并 联,电源中的电流不确定。 _ + uS1 _ + uS2 _ i + u _ ③电压源与支路的串、并联等效 + uS1 _ + uS2 _ uS + _ R i R2 i R1 _ _ u + u + u  us1  R1i  us 2  R2i  (uS 1  uS 2 )  ( R1  R2 )i  uS  Ri i uS + _ 任意 元件 + u R _ uS 对外等效！ + _ i + u _ 2. 理想电流源的串联并联 注意参考方向 i  is1  is 2      isn   isk ①并联 i iS2 iS1 iSn ②串联 i 等效电路 等效 i  is1  is 2 路 电 iS1 iS2 i 注意 相同的理想电流源才能串联, 每个电 流源的端电压不能确定。 3.电流源与支路的串、并联等效 i iS1 iS2 R1 + R2 u 等效电路 _ iS R i  is1  u R1  is 2  u R2  is1  is 2  (1 R1  1 R2 )u  is  u R 任意 元件 iS + u R _ iS 等效电路 对外等效！ 5 实际电源的两种模型及其等效变换 1. 实际电压源 伏安特性： i u + + uS _ u RS u  uS  RS i us 考虑内阻 0 一个好的电压源要求 i RS  0 注意 实际电压源也不允许短路。因其内阻小， 若短路，电流很大，可能烧毁电源。 2. 实际电流源 i RS + iS u u _ 考虑内阻 u 伏安特性： i  i  S RS is 0 i 一个好的电流源要求 RS   注意 实际电流源也不允许开路。因其内阻大， 若开路，电压很高，可能烧毁电源。 3.电压源和电流源的等效变换 实际电压源、实际电流源两种模型可以进行等效 变换，所谓的等效是指端口的电压、电流在转换过 程中保持不变。 + i+ i uS 实际 实际 + _ iS u 电流 电压 GS u RS _ 源 源 _ 端口特性 i =iS – GSu iS=uS /RS GS=1/RS u=uS – RS i i = uS/RS– u/RS 比较可得等效条件 小结 电压源变换为电流源： i + uS _ RS i+ i S 转换 + u _ GS u _ 电流源变换为电压源： i 转换 + iS GS u _ + uS _ RS i+ u _ + 注意 ①变换关系 uS _ RS i+ i u _ i iS iS GS iS + u _ 数值关系 方向：电流源电流方向与电压源电压方向相反。 ②等效是对外部电路等效，对内部电路是不等效的。 表 现 在  电压源开路， RS上无电流流过 电流源开路， GS上有电流流过。  电压源短路， RS上有电流； 电流源短路, GS上无电流。 ③理想电压源与理想电流源不能相互转换。 例1 利用电源转换简化电路计算 1. 5A 2A 2. 5 + 10V _ 3 4 + 10V _ I＝？ 7 + 15V _ 5 + U=？ 6A _ 7 I=0.5A 7 8V + 2A 6A U=20V + 2.5 U _ 例2 把电路转换成一个电压源和一个电阻的串连 1. 10V + _ 6A + 10V _ 10 2. + 6V _ 10 2A 6A 10 + 70V _ 10 + 66V _ 1. 10V + _ 6A + 10V _ 1A 10 10 7A 6A + 10 _ 70V 10 2. + 6V _ 10 2A 6A + 6V _ 10 + _60V + 6V _ 6A 10 10 + 66V _ 例3 求电路中的电流I 2A 10 10 + 40V _ 6 I 6 I 2A 10 4 + 2A 30V _ + 40V _ 6 30  60 I  1.5A 20 10 + 60V _ I 4 + 30V _ 4 + 30V _ 例4 求电流 i1 R2 R3 R  R1  R2  R3 Ri1  ( R2 // R3 )ri1 / R3  U S US i1  R  ( R2 // R3 )r / R3 注意 受控源和独立 源一样可以进行电源转 换；转换过程中注意不 要丢失控制量。 R1 + US _ R3 i1 i1 i 1 R R2 ri1 + _ ri1/R3 + + 1 R + US (R2//RR32)ri //R13/R3 _ _ 例5 把电路转换成一个电压源和一个电阻的串联 1k + 1k 10V 0.5I _ I 500I -I 2k + + U _ U  500 I  2000 I  10  1500 I  10 + 10V _ 1.5k + 10V _ + U _ I + U _ 6 输入电阻 1.定义 2.计算方法 无 源 i + u - 输入电阻 u Rin  i ①如果一端口内部仅含电阻，则应用电阻的串、并联 和—Y变换等方法求它的等效电阻； ②对含有受控源和电阻的两端电路，用电压、电流法 求输入电阻，即在端口加电压源，求得电流，或在 端口加电流源，求得电压，得其比值。 例 计算下例一端口电路的输入电阻 1. R2 i1 R1 uS 解 + R3 i2 R2 R1 R3 无源电 阻网络 _ 先把有源网络的独立源置零：电压源短路； 电流源开路，再求输入电阻。 Rin  ( R1  R2 ) // R3 2. 6 － 6i1 + 6 + 3 US _ i1 3i1 i  i1   1.5i1 6 U  6i1  3i1  9i1 U 9i1 Rin    6Ω i 1.5i1 i1 － 3 6i1 + i + _ U 外加电 压源 3. i2 0.1u1 5 i1 + u1 _ 等效 10 + 15 u － i i  i1  i2  2.5i1 u  5i  u1  5  2.5i1  15i1  27.5i1 u 27.5i1 Rin    11Ω i 2.5i1 5 + u1 _ u1  15i1 i2  0.1u1  1.5i1 15 10  15 Rin  5   11Ω 10  15