岩石疲劳破坏的变形控制律、岩土力学试验的实时X射线CT扫描和边坡坝基....pdf

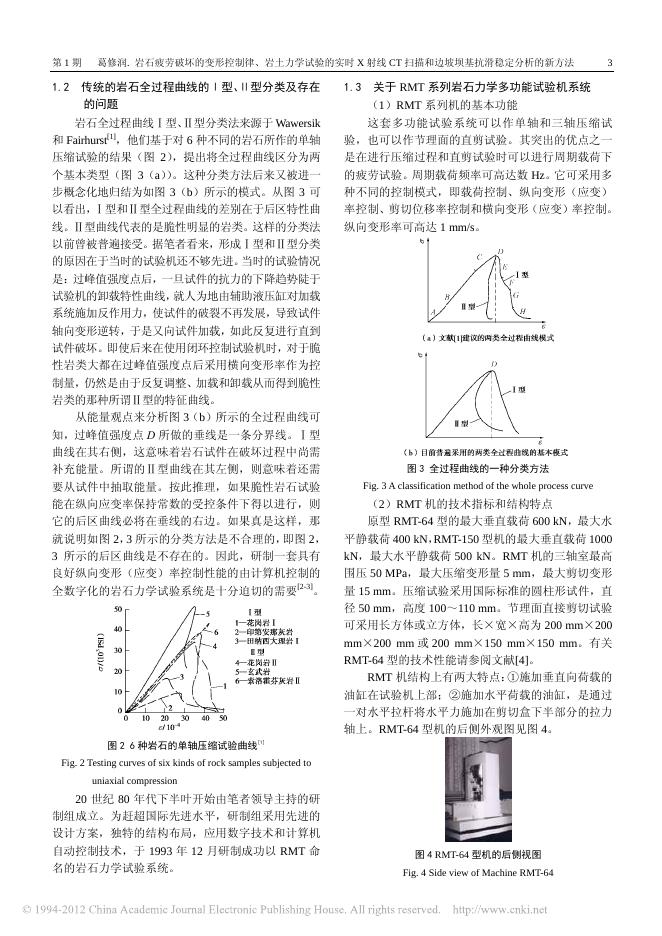
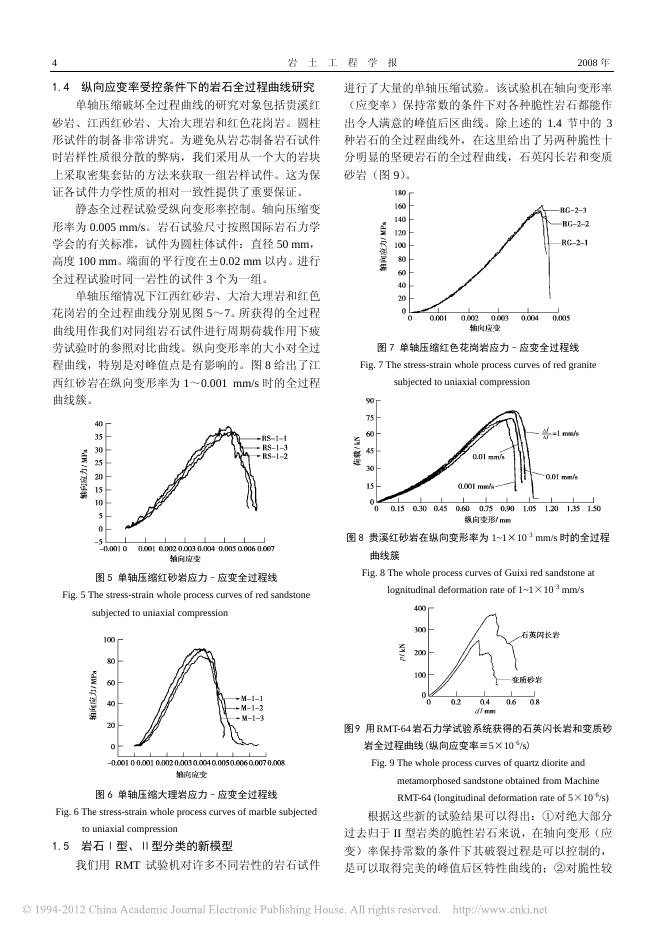
第 30 卷 2008 年 第1期 1月 岩 土 工 程 学 报 Chinese Journal of Geotechnical Engineering Vol.30 No.1 Jan., 2008 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 葛修润 (1.中国科学院武汉岩土力学研究所，湖北 武汉 430071；2.上海交通大学岩土力学与工程研究所，上海 200030；3.岩土力学与 工程国家重点实验室，湖北 武汉 430071) 摘 要：介绍了近年来在岩土力学领域方面取得的一些进展:①关于岩石疲劳破坏试验 方面的实验结果。大量的试验清楚表明岩石发生疲劳破坏时的变形量受岩石应力-应变 全过程曲线控制的规律，介绍了这方面的试验技术及新型的岩石力学试验机——RMT 机的特性，对岩石的 I 型和Ⅱ型分类作了评述。岩石疲劳试验结果也提示我们在研究 岩石的强度理论时要特别重视从变形角度去探讨。②简要介绍了岩土力学室内试验方 面的一项新的实验技术——实时 X 射线 CT 扫描的试验方法和原理。重点给出了南桥 砂岩三轴试验的结果，并与典型的全过程曲线作了对比分析。这一新技术为岩土力学 界提供了一种新手段，使宏观的力学性能与细观层次上的结构演变和裂纹萌生、扩展 直到破坏有机地联系起来，为损伤研究提供了一种新的实验手段。③论述了采用强度 储备概念求抗滑稳定安全系数方面的不足之处。基于力是矢量这一基本概念，提出了 计算抗滑稳定安全系数的新方法——矢量和分析方法，并与传统分析方法作了对比， 指出了这种新方法的优点。除了平面问题外，还论述了三维问题的计算方法和算式。 关键词：岩土力学；周期荷载；疲劳；不可逆变形；应力–应变全过程曲线；损伤扩 展机理；CT 实时试验；边坡与坝基；抗滑稳定分析；矢量和分析法；安全系数 中图分类号：TU45 文献标识码：A 文章编号：1000–4548(2008)01–0001–20 作者简介：葛修润（1934– ），男，上海市人，岩土力学专家，中国工程院院士。1959 年毕业于原苏联敖德萨建筑工 程学院水利系。主要从事岩体工程问题和数值分析方法、测试技术及岩体基本力学性质等研究。参加我国最早结合大 型原位试验的大冶铁矿南邦边坡研究，1967 年独立主持完成了该工程边坡稳定分析和岩体力学试验总结。主持了大冶 北邦滑坡整治、铜绿山、永平、海南等大型矿山边坡工程，社会、经济效益显著。70 年代初进行的 511 工程地下洞群 非线性分析是国内大型地下工程应用有限元首例。为葛洲坝二江泄水闸作抗滑稳定非线性分析，清江隔河岩重力拱坝 连同复杂岩基的三维有限元分析等，均为解决工程难题作出重大贡献。1993 年研制成功总体性能具有国际领先水平的 液压伺服岩石力学多功能试验机。近年来为长江三峡水利枢纽、水布垭水电站、小湾水电站和深圳地铁建设作出贡献。 2001 年为位于三峡水库库底的白鹤梁古水文题刻原址水下保护工程提出原创性方案，被国家采纳，目前正在施工。 Deformation control law of rock fatigue failure, real-time X-ray CT scan of geotechnical testing, and new method of stability analysis of slopes and dam foundations GE Xiu-run (1. Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China; 2. Institute of Geotechnical Engineering, Shanghai Jiao Tong University, Shanghai 200030, China; 3. State Key Laboratory of Geomechanics and Geotechnical Engineering, Wuhan 430071, China) Abstract: Some progresses were presented on the field of rock and soil mechanics for the past few years. Firstly, the test results of rock fatigue failure were discussed. A lot of tests have shown that the strain of fatigue failure is controlled by the whole stress-strain process curve. The testing techniques and the characteristics of the new testing machine for rock mechanics, ─────── 收稿日期：2007–12–15 岩 2 土 工 程 学 报 2008 年 RMT were introduced. The post-failure curves of type I and type II for rock were reviewed. More emphasis should be paid on the deformations in rock strength theory research based on the rock fatigue failure tests. Secondly, the creative testing technique in rock and soil mechanics experiments, the X-ray computerized tomography (CT) real-time scan was presented. The testing principles and methods were given. The triaxial testing results of Nanqiao sandstone were discussed. The whole stress-strain process curve of Nanqiao sandstone was obtained, and comparison between the former and the typical whole process curve was analyzed. A new approach was provided for rock and soil mechanics, and it connected the macro-mechanical properties of rock materials with the meso-structures including the compression and growth of microcracks, bifurcation, and crack fracture. Thirdly, the vector sum method of stability analysis for dam foundation and slope was given. The safety factor by the vector sum method was defined based on the vector characteristics of the forces. The significance of the vector sum method safety factor was clear in physics. The calculating process was simple, and it facilitated the application of this analysis method in engineering. The 2D slope calculation models with fixed circle slip surface, non-circle slip surface and curved slip surface were discussed. The results indicate that the safety factor obtained by vector sum method is in good agreement with the safety factors obtained by the limit equilibrium method. It is shown that the new method is more stable. The calculation formula of safety factor for the 3D problem by vectors sum method is also given. Key word: rock and soil mechanics; cyclic loading; fatigue; irreversible deformation; complete stress-strain curve; damage propagation law; CT real-time testing; slope and dam foundation; analyses of stability against sliding; vector sum analysis method; safety factor 0 前 言 介绍了岩土力学研究领域内 3 项新的进展：①岩 石力学室内试验，特别是岩石应力–应变全过程曲线 的研究和岩石疲劳破坏受静态全过程曲线控制的规 律。②一项新的试验技术，利用医用 X 射线 CT 机为 岩土力学室内试验作实时检测。即在开展岩土力学室 内单轴和三轴试验时能实时或同步地用 CT 扫描技术 来窥探试样内部裂缝的萌生、扩展演变成大的裂面最 后试件整个崩溃的全过程，这项新的试验技术提供了 一种新手段和可能性，使宏观的力学性能与细观层次 上的结构演变过程联系起来，为损伤的演变过程提供 佐证，为认识和总结损伤演变规律提供一种方法。③ 提出一种新的抗滑稳定问题的分析方法—— “矢量和” 抗滑稳定分析新方法。 1 岩石疲劳破坏受控于岩石全过程曲 线的规律 对 1970 年国外提出的全过程线及岩石Ⅰ型、Ⅱ型 分类模型作了简要介绍，并提出不同见解，阐述这种 分类的不合理性并分析这种不合理的Ⅱ型曲线产生的 原因所在。笔者认为，只有在纵向应变率受控条件下 才能获得科学的岩石全过程曲线。笔者等用了将近 8 a 的时间研制了性能十分良好的由计算机进行伺服控制 的全数字化的岩石力学试验系统——RMT 系列试验 机，介绍了它的基本性能，并给出了包括世界上 3 大 岩类在纵向应变率受控条件下的岩石全过程曲线。在 科学的全过程曲线的基础上，提出了岩石Ⅰ型、Ⅱ型 分类的新模型。利用 RMT 机进行了数量很多的在周 期荷载作用下的岩石疲劳试验。试验结果表明，岩石 的疲劳破坏完全受它静态的全过程曲线所控制，得出 了疲劳破坏的基本规律。 1.1 岩石全过程曲线 岩石全过程曲线指的是对岩石的标准试件（直径 5 cm，长度 10～11 cm）进行单轴压缩试验时所获得的包 括峰值强度以前区域和以后区域在内的轴向应力（荷 载）和轴向应变（变形）的关系曲线，其概念性的曲线 见图 1。图 1 中的 D 点，也称峰值强度点 P。OA 段为 初始压缩段，AB 为线性段，即弹性阶段。B 点为比例 极限点，稍上面一点可称为屈服限，为了简化通常可以 不区分它们。BD 段为非线性变形段。BD 段又可分 BC 和 CD 段。在 BC 段内非线性变化还不十分显著，但在 CD 段内变化激烈，伴随着试件的内部破坏。D 点即为 岩石的峰值强度，将整个曲线分为峰前区和峰后区。对 于韧性较好的岩石很容易得到 E 点，即残余强度点，对 于脆性明显的岩类在一般试验机上不容易获得峰后区。 图 1 岩石静载全过程曲线示意图 Fig. 1 Stress-strain whole process curve for rock subjected to static loading 第1期 1.2 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 传统的岩石全过程曲线的Ⅰ型、Ⅱ型分类及存在 的问题 岩石全过程曲线Ⅰ型、 Ⅱ型分类法来源于 Wawersik [1] 和 Fairhurst ，他们基于对 6 种不同的岩石所作的单轴 压缩试验的结果（图 2） ，提出将全过程曲线区分为两 个基本类型（图 3（a） ） 。这种分类方法后来又被进一 步概念化地归结为如图 3（b）所示的模式。从图 3 可 以看出，Ⅰ型和Ⅱ型全过程曲线的差别在于后区特性曲 线。Ⅱ型曲线代表的是脆性明显的岩类。这样的分类法 以前曾被普遍接受。据笔者看来，形成Ⅰ型和Ⅱ型分类 的原因在于当时的试验机还不够先进。当时的试验情况 是：过峰值强度点后，一旦试件的抗力的下降趋势陡于 试验机的卸载特性曲线，就人为地由辅助液压缸对加载 系统施加反作用力，使试件的破裂不再发展，导致试件 轴向变形逆转，于是又向试件加载，如此反复进行直到 试件破坏。即使后来在使用闭环控制试验机时，对于脆 性岩类大都在过峰值强度点后采用横向变形率作为控 制量，仍然是由于反复调整、加载和卸载从而得到脆性 岩类的那种所谓Ⅱ型的特征曲线。 从能量观点来分析图 3（b）所示的全过程曲线可 知，过峰值强度点 D 所做的垂线是一条分界线。Ⅰ型 曲线在其右侧，这意味着岩石试件在破坏过程中尚需 补充能量。所谓的Ⅱ型曲线在其左侧，则意味着还需 要从试件中抽取能量。按此推理，如果脆性岩石试验 能在纵向应变率保持常数的受控条件下得以进行，则 它的后区曲线必将在垂线的右边。如果真是这样，那 就说明如图 2，3 所示的分类方法是不合理的，即图 2， 3 所示的后区曲线是不存在的。因此，研制一套具有 良好纵向变形（应变）率控制性能的由计算机控制的 全数字化的岩石力学试验系统是十分迫切的需要[2-3]。 1.3 关于 RMT 系列岩石力学多功能试验机系统 （1）RMT 系列机的基本功能 这套多功能试验系统可以作单轴和三轴压缩试 验，也可以作节理面的直剪试验。其突出的优点之一 是在进行压缩过程和直剪试验时可以进行周期载荷下 的疲劳试验。周期载荷频率可高达数 Hz。它可采用多 种不同的控制模式，即载荷控制、纵向变形（应变） 率控制、剪切位移率控制和横向变形（应变）率控制。 纵向变形率可高达 1 mm/s。 图 3 全过程曲线的一种分类方法 Fig. 3 A classification method of the whole process curve （2）RMT 机的技术指标和结构特点 原型 RMT-64 型的最大垂直载荷 600 kN，最大水 平静载荷 400 kN， RMT-150 型机的最大垂直载荷 1000 kN，最大水平静载荷 500 kN。RMT 机的三轴室最高 围压 50 MPa，最大压缩变形量 5 mm，最大剪切变形 量 15 mm。压缩试验采用国际标准的圆柱形试件，直 径 50 mm，高度 100～110 mm。节理面直接剪切试验 可采用长方体或立方体，长×宽×高为 200 mm×200 mm×200 mm 或 200 mm×150 mm×150 mm。有关 RMT-64 型的技术性能请参阅文献[4]。 RMT 机结构上有两大特点：①施加垂直向荷载的 油缸在试验机上部；②施加水平荷载的油缸，是通过 一对水平拉杆将水平力施加在剪切盒下半部分的拉力 轴上。RMT-64 型机的后侧外观图见图 4。 图 2 6 种岩石的单轴压缩试验曲线[1] Fig. 2 Testing curves of six kinds of rock samples subjected to uniaxial compression 20 世纪 80 年代下半叶开始由笔者领导主持的研 制组成立。为赶超国际先进水平，研制组采用先进的 设计方案，独特的结构布局，应用数字技术和计算机 自动控制技术，于 1993 年 12 月研制成功以 RMT 命 名的岩石力学试验系统。 3 图 4 RMT-64 型机的后侧视图 Fig. 4 Side view of Machine RMT-64 岩 4 1.4 土 纵向应变率受控条件下的岩石全过程曲线研究 单轴压缩破坏全过程曲线的研究对象包括贵溪红 砂岩、江西红砂岩、大冶大理岩和红色花岗岩。圆柱 形试件的制备非常讲究。为避免从岩芯制备岩石试件 时岩样性质很分散的弊病，我们采用从一个大的岩块 上采取密集套钻的方法来获取一组岩样试件。这为保 证各试件力学性质的相对一致性提供了重要保证。 静态全过程试验受纵向变形率控制。轴向压缩变 形率为 0.005 mm/s。岩石试验尺寸按照国际岩石力学 学会的有关标准，试件为圆柱体试件：直径 50 mm， 高度 100 mm。端面的平行度在±0.02 mm 以内。进行 全过程试验时同一岩性的试件 3 个为一组。 单轴压缩情况下江西红砂岩、大冶大理岩和红色 花岗岩的全过程曲线分别见图 5～7。所获得的全过程 曲线用作我们对同组岩石试件进行周期荷载作用下疲 劳试验时的参照对比曲线。纵向变形率的大小对全过 程曲线，特别是对峰值点是有影响的。图 8 给出了江 西红砂岩在纵向变形率为 1～0.001 mm/s 时的全过程 曲线簇。 工 程 学 报 2008 年 进行了大量的单轴压缩试验。该试验机在轴向变形率 （应变率）保持常数的条件下对各种脆性岩石都能作 出令人满意的峰值后区曲线。除上述的 1.4 节中的 3 种岩石的全过程曲线外，在这里给出了另两种脆性十 分明显的坚硬岩石的全过程曲线，石英闪长岩和变质 砂岩（图 9） 。 图 7 单轴压缩红色花岗岩应力–应变全过程线 Fig. 7 The stress-strain whole process curves of red granite subjected to uniaxial compression 图 8 贵溪红砂岩在纵向变形率为 1~1×10-3 mm/s 时的全过程 曲线簇 图 5 单轴压缩红砂岩应力–应变全过程线 Fig. 8 The whole process curves of Guixi red sandstone at - Fig. 5 The stress-strain whole process curves of red sandstone lognitudinal deformation rate of 1~1×10 3 mm/s subjected to uniaxial compression 图 9 用 RMT-64 岩石力学试验系统获得的石英闪长岩和变质砂 岩全过程曲线(纵向应变率≡5×10-6/s) Fig. 9 The whole process curves of quartz diorite and metamorphosed sandstone obtained from Machine 图 6 单轴压缩大理岩应力–应变全过程线 Fig. 6 The stress-strain whole process curves of marble subjected to uniaxial compression 1.5 岩石Ⅰ型、Ⅱ型分类的新模型 我们用 RMT 试验机对许多不同岩性的岩石试件 - RMT-64 (longitudinal deformation rate of 5×10 6/s) 根据这些新的试验结果可以得出：①对绝大部分 过去归于 II 型岩类的脆性岩石来说，在轴向变形（应 变）率保持常数的条件下其破裂过程是可以控制的， 是可以取得完美的峰值后区特性曲线的；②对脆性较 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 明显的岩石而言，其后区曲线一般都较陡，并且局部 有小台阶，这是破裂局部受阻的缘故；③新的试验结 果表明前述的传统的 II 型曲线的不合理性， 那种Ⅰ型、 Ⅱ型分类方法也是不合适的。 根据最新的试验结果，我们建议采用图 10 所示的 模式作为岩石峰值后区特性曲线和全过程曲线的新模 型[5]。此新模型以过峰值强度点 D 所作的垂直线为极 限线，在轴向变形（应变）率保持常数条件下，岩石 的后区特性曲线均在其右侧。 越是脆性的岩石其峰值后区曲线的坡度（指绝对 值）越陡，即越逼近极限线，且其曲线上有明显的台 阶状。这是由于突然的局部破裂造成抗力急剧下降和 破裂传播受阻等复杂因素形成的。韧性越大的岩石其 后区特性曲线的坡度越平缓。 在做数值分析时，我们认为对于脆性十分明显的 岩类峰后曲线可以作为接近极限线，过峰值强度点后 简化为作垂直跌落到残余强度点，并提出了一整套基 于理想脆性的脆塑性分析方法[6]。如果峰后曲线有坡 度，也可以作为非理想脆性，这些相应的分析方法可 参见文献[7]。 5 如进行周期荷载作用下的岩石单轴压缩试验时如轴向 应力值低于此门槛值时，虽然经过数万次的周期荷载 试验岩石不会发生疲劳破坏。因此，这可以作为工程 中岩石不发生疲劳破坏的标准，当然还需给以一定的 安全裕度，即最大轴向应力控制在不超过 B 点应力值 的 90%为宜。 图 11 周期加载波形 Fig. 11 Cyclic loading wave 图 12 门槛值示意图 Fig. 12 Sketch map of threshold value 图 10 岩石全过程分类曲线的新模型 Fig. 10 The new model of whole process classification curve of rock 1.6 周期载荷作用下岩石疲劳试验 岩石在周期载荷作用下疲劳试验是以载荷控制， 加载波形为正弦波，频率 0.2 Hz。周期载荷的加载波 形如图 11 所示。 ∆σ = σ max − σ min ， (1) f = 1/ T ， (2) 式中， σ max 为周期荷载的上限应力， σ min 为周期荷载 的下限应力，∆σ 为周期荷载的幅值，T 为周期， f 为 频率。 疲劳试验的控制因素包括上限应力、下限应力、 频率、幅值、周期载荷循环次数和波形等。 周期荷载作用下岩石的疲劳特性还受到门槛值的 影响，当周期荷载的上限应力值低于某数值时，即使 周期荷载循环次数再多岩石也不会破坏，我们曾对此 门槛值做过详细研究[8-9]。图 12 是说明如何决定门槛 值的方法示意图。试验结果可知，门槛值实际上就是 岩石全过程曲线线性阶段与非线性阶段的分界点 B。 岩石疲劳破坏试验曲线如图 13 所示。图中 C 点 称之为该块岩石试件的疲劳破坏点。如将上限应力作 一水平线与这类岩石的静态全过程曲线相交，此交点 称为由全过程曲线控制岩石疲劳破坏的控制点。为了 能分辨出疲劳试验的滞环线，规定轴向变形增长量达 到 0.015 mm 时，才画一个滞环线。实际上达到疲劳 破坏时的滞环数或周期荷载循环次数 N f 记录在文件 中， 试验中已进行了的循环次数随时显示在监视屏上。 图 13 疲劳破坏试验曲线 Fig. 13 Fatigue failure testing curve 疲劳试验分如下 4 种情况进行：①甲类，疲劳试 验从峰值前区开始，周期荷载的上限应力＞门槛值， 但幅值恒定。②乙类，疲劳试验从峰值前区开始，上 岩 6 土 工 限应力＞门槛值，但幅值不保持常数。第一阶段幅值 小，第二阶段幅值大。③丙类，疲劳试验从峰值后区 某个位置开始。或先进行主动卸载，然后再加载，最 后进行疲劳试验。④丁类，疲劳试验从峰值前区开始， 但上限应力 σ max ＜门槛值。对此情况我们做过许多次 试验。周期荷载次数达数万次，但轴向变形量仍然非 常小、完全不发生疲劳破坏。 （1）岩石的基本疲劳试验（甲类试验） 对贵溪红砂岩、江西红砂岩、大冶大理岩和红色 花岗岩进行了数量很多的疲劳破坏试验。前两种砂岩 属沉积岩类，大冶大理岩为典型的变质岩类，花岗岩 为火成岩类。试验结果见图 14～17。 程 学 报 2008 年 图 15 江西红砂岩#RS-4-1 疲劳试验曲线 Fig. 15 Fatigue test curve of Jiangxi red sandstone specimen # RS-4-1 图 16 大冶大理岩#M-2-1 试件疲劳试验曲线 图 14 贵溪红砂岩疲劳试验 Fig. 16 Fatigue test curve of Daye marble specimen #M-2-1 Fig. 14 Fatigue test curve of Guixi red sandstone 从图中可看出周期荷载试验的岩石破坏点与全过 程曲线的相应控制点非常接近，即岩石疲劳破坏受静 态全过程曲线控制。 表 1 给出了 12 个岩石试件的疲劳 破坏试验结果，表中上限应力比即 σ max 与峰值强度 P 之比，下限应力比即 σ min 与峰值强度 P 之比。 （2）复杂加载幅值变化情况下的疲劳试验 复杂加载幅值变化情况下的疲劳试验有 3 种情 况：①变幅疲劳试验，江西红砂岩试件#RS-14-3 的试 验结果（图 18）可以看出，即便采用变幅，但发生疲 劳破坏时仍然受静态全过程曲线控制；②峰后曲线段 的周期荷载试验结果如图 19 所示； ③在峰后曲线段卸 载，再加载后的岩石周期疲劳破坏试验如图 20 所示。 图 17 红色花岗岩#RG-5-3 试件疲劳试验曲线 Fig. 17 Fatigue test curve of red granite specimen #RG-5-3 （3）上限应力、下限应力变动时的试验情况 上限应力、下限应力变动时的试验情况为：① σ max 表 1 周期荷载作用下岩石疲劳破坏试验结果 Table 1 Fatigue failure test results of rock subjected to cyclic loading 岩 性 红 砂 岩 大 理 岩 红 色 花 岗 岩 编号 RS-3-1 RS-3-3 RS-5-1 RS-4-1 M-2-1 M-3-1 M-3-3 RG-1-1 RG-3-1 RG-4-2 RG-4-1 RG-5-3 上限应 力/MPa 33.9 33.9 32.0 30.2 81.1 76.6 76.6 141.3 141.3 141.3 141.3 125.6 下限应 力/MPa 11.3 11.3 11.3 11.3 27.0 27.0 27.0 47.1 62.8 78.5 78.5 47.1 幅值 /MPa 22.6 22.6 20.7 18.9 54.1 49.6 49.6 94.2 78.5 62.8 62.8 78.5 上限应 力比 0.91 0.91 0.86 0.82 0.92 0.87 0.87 0.90 0.90 0.90 0.90 0.80 下限应 力比 0.31 0.31 0.31 0.31 0.31 0.31 0.31 0.30 0.40 0.50 0.50 0.30 疲劳寿 命/次 691 114 508 8458 744 372 507 30 174 113 629 6072 破坏点 应变 5.6340×10 3 5.9804×10 3 5.4024×10 3 5.3241×10 3 4.3623×10 3 4.0645×10 3 5.1505×10 3 4.8434×10 3 4.8789×10 3 4.9780×10 3 5.7181×10 3 4.7594×10 3 控制点 应变 5.4146×10 3 5.4146×10 3 5.5128×10 3 5.4208×10 3 4.5271×10 3 4.7948×10 3 4.7948×10 3 5.2710×10 3 5.2710×10 3 5.2710×10 3 5.2710×10 3 5.1969×10 3 偏差 - 0.1488×10 3 0.5658×10 3 -0.1104×10 3 -0.0967×10 3 -0.1648×10 3 -0.7303×10 3 -3 0.3557×10 -0.4276×10 3 -0.3921×10 3 -3 -0.293×10 0.4471×10 3 -0.4429×10 3 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 7 变质岩类，火成岩类）都适用。③在三轴压缩情况下， 全过程曲线是对应于相应的 σ 3 求得的，变形控制律不 变。④各种影响因素不改变变形控制律，但对发生疲 劳破坏时的总周期数有影响。⑤周期荷载的上限应力 低于门槛值时，从工程角度讲，一般不会发生岩石疲 劳破坏。⑥轴向应变（变形）的发展一般具有明显的 三阶段特征（图 24） ，与流变变形的三阶段十分相似。 图 18 #RS-14-3 江西红砂岩变幅疲劳试验曲线 Fig. 18 Fatigue test curve of Jiangxi red sandstone specimen # RS-14-3 at variable amplitudes 图 19 江西红砂岩#RS-6-1 试件峰后疲劳试件 Fig. 19 Fatigue test curve of Jiangxi red sandstone specimen # RS-6-1 after peak 图 21 贵溪红砂岩试件上限相同、幅值不同（a），上限不同、 幅值相同（b）时的疲劳试验 Fig. 21 Fatigue test curves of Guixi red sandstone specimens with the different upper limits or different amplitudes 图 20 贵溪红砂岩峰值后区疲劳试验 Fig. 20 Fatigue test curve of Guixi red sandstone after peak 保持不变，σ min 不同时的试验结果（图 21（a） ） ；② σ min 保持不变，或 σ max 不同时的试验结果（图 21（b） ） 。 （4）三轴压缩条件下的疲劳破坏试验 有关三轴试验给出江西红砂岩三轴压缩疲劳破坏 试验的两个结果（图 22） 。 1.7 岩石疲劳破坏的变形控制律 有关周期荷载波形、频率等方面的试验，试验情 况、结果和规律可参考文献[10]。综合结果可得出一 张概念性示意图如图 23 所示。 岩石疲劳破坏的变形规律可表述如下：①岩石的 疲劳破坏完全受到静态全过程曲线的控制。疲劳破坏 的极限应变（变形）即为周期荷载上限应力（荷载） 水平线所对应的静态全过程曲线的应变（变形）总量。 ②岩石疲劳破坏的变形控制律对于全部岩类 （沉积岩， 图 22 江西某地红砂岩三轴压缩的疲劳试验曲线与静态全过程 曲线的关系图 Fig. 22 Relationship between fatigue test curve and the static whole process curve of Jiangxi red sandstone subjected to triaxial compression 岩 8 土 工 程 学 报 2008 年 供了一种新技术，为深入研究岩土力学的损伤演化理 论提供了新手段。相关研究见文献[11～15]。以下除 介绍 CT 试验的简要概念外，重点将放在介绍陕西蒲 白矿务局南桥煤矿的砂岩在单轴和三轴压缩荷载作用 下损伤扩展机理的 CT 试验和所得的结果。有关其他 方面的试验情况请参阅文献[12，16～21]。 2.1 X 射线 CT 实时检测试验和设备 图 23 岩石疲劳破坏受静态全过程控制概念图 Fig. 23 Concept map of rock fatigue failure controlled by static whole process 图 24 大冶大理岩 M-3-1 试件轴向变形三阶段发展曲线 Fig. 24 Three stages evolution curve of axial deformation of Daye marble specimen M-3-1 1.8 研究周期荷载作用下岩石疲劳破坏变形控制律 的意义 研究的意义在于：①是不同岩类的普遍规律；② 为疲劳寿命的评估奠定了基础，在工程应用上具有很 重要的价值；③此规律提示我们，从变形的角度去研 究岩石的破坏和强度理论有十分重要的意义；④此规 律也意味着疲劳破坏与流变破坏似乎是“同源”的； ⑤用疲劳试验去研究流变强度与破坏似乎也是一种可 以尝试的途径。 2 岩土力学实验研究中的 X 射线 CT 实 时扫描新技术 X 射线 CT 实时扫描新技术是由笔者提出设想和 主持设计的，1999 年在中国科学院寒区旱区环境和工 程国家重点实验室研制成功的岩土力学专用三轴加载 设备上进行的。它可以用于进行三轴和单轴压缩试验 全过程的岩石细观损伤扩展的 CT 实时扫描试验，探 求岩石破坏机理。对黏土、冻土、冻岩和冰试件均适 用。这样的试验技术从细观层面上给岩土力学试验提 （1）关于 CT 检测基本原理和 CT 机 目前，国内外在岩石损伤细观损伤检测方面的检 测手段有如下两大方面：①带有加载装置的光学显微 镜和扫描电镜；②计算机断层扫描技术（computerized tomography）——CT 技术。扫描电镜或光学显微镜检 测的缺陷是试件太小，切片扰动，单轴加载，加载太 小，单一观测断面和力学机制不明确。CT 检测的优 势是可以进行多层断面观测，加载荷载大，可采用国 际标准圆柱型试样，可以立体成像。目前国内外已有 的岩石损伤 CT 检测工作存在缺陷是：先在试验机上 做宏观试验，在试验进行到一定阶段终止试验，然后 将试件放在 CT 机扫描。显然，卸载对 CT 试验结果 有明显的影响，而且无法将宏观试验过程连续进行并 且无法对裂纹演化情况进行实时扫描。 1969 年， Housfield 建立了医用 CT 机的标准方程： µrm − µH2o H rm = 1000 × ， (3) µH o 2 式中， H rm 为 CT 数， µrm 为某图像点物体的 X 射线 吸收系数， µH2 o 为纯水的 X 射线吸收系数，也可简写 为 µw 。 从式（3）可以看出，Housfield 建立了以纯水 CT 数为 0 的理想图像标准，在此标准下，某点对 X 射线 的吸收强弱直接用 CT 数表示出来。如果被测体是仅 存在密度 ρ 变化的同一种物质（其单位密度质量吸收 系数为 µm ） ，被检测物质对 X 射线的吸收系数为 µrm = µm ρ ， (4) 令 µ w = 1 ，得 H rm +1 ρ = 1000 ， (5) µm 从式（5）看出，在已知这种物质的 X 射线吸收系数 µm 的条件下，CT 数就直接表示了物质的密度 ρ ，简言 之，CT 图像就是被测体某层面的密度图。 我们使用的 CT 机为 SIEMENS SOMATOM plus 型 X 射线螺旋 CT 机，空间分辨率是 0.35 mm×0.35 ， mm，可识别的最小体积为 0.12 mm3（厚度 1 mm） 密度对比分辨率为 0.3%（3Hu） 。细观力学研究对象的 -1 尺度可以从 10 nm 到 mm。采用上述 CT 机进行岩石 细观损伤扩展规律试验可满足细观力学尺度的下限。 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 （2）与 CT 机配套的专用岩土三轴试验装置 新研制的 CT 专用三轴试验机外形为 240 mm× 1000 mm，试验仓内径 142 mm，最大轴向压力设计为 400 kN，围压为 20 MPa，轴向工作行程 40 mm，位移 传感器量程 0～50 mm，精度是 0.31%。此试验系统可 对国际标准圆柱形岩石试件进行 CT 实时破坏试验， 岩石试件尺寸为Φ 50 mm× 100 mm 。也可对Φ 61.8 mm×150 mm 的土样进行破坏试验。用 CT 机进行实 时扫描，可研究试验全过程中试件的变形破坏情况。 由于试验仓将放在 CT 机的扫描区，为减少试验仓体 材料对 CT 扫描结果的影响，试验仓不能用重金属材 料制作，故试验仓采用优质的轻金属材料 LY12 加工 而成。岩土损伤 CT 试验装置原理示意图见图 25，CT 加载设备与试验方法示意图见图 26，试样安装桶原理 图见图 27。 9 线就可以知道整个过程中 CT 图的变化和测得的 CT 数的变化情况。这就也提供了岩石从微孔洞被压密到 微裂纹发生、分叉、发展、断裂破坏直到卸荷各个阶 段的清晰图像。而这些裂缝发展过程也正好与岩石全 过程曲线的各个阶段相适应，从而从细观的角度给出 了宏观力学机制的物理解释。 图 27 试样安装桶原理图 Fig. 27 Principle of installing specimen vessel 2.3 图 25 岩土损伤 CT 试验装置原理示意图 南桥砂岩 X 射线 CT 实时扫描试验 （1）试验情况简介 试件采用陕西蒲白矿务局南桥煤矿的砂岩，平均 密度 2.45 g/cm3，以#5 试件为例。在三轴试验的试件 从上到下设定 4 个层位，在加载过程中的各个阶段对 各层位进行实时 CT 扫描，观察各断面裂纹的萌生、 分叉、发展、断裂和卸载全过程的图象变化，从细观 尺度研究岩石的破坏机理。应变速率是 2.79×10 5/s， 试验耗时 55 min。#5 试件分 4 个扫描层，扫描层厚 3 mm。试验过程中进行 8 次扫描，共得 32 幅图像。试 件中的 4 个扫描断面位置如图 28 所示。 Fig. 25 Principle of special triaxial loading testing equipment 图 26 试验装置与三轴试验机 Fig. 26 Testing equipment of CT machine and triaxial cell 2.2 试验方法 将专用的三轴试验装置水平安放在 CT 机的活动 试验台上，试样安放在三轴试验装置腔体内。活动试 验台放置的位置以试样正好处在 CT 机扫描范围之内 为宜。随着轴向荷载增大到某一值时，CT 机对于试 件预先设定的几个断面进行扫描，就可以获得这几个 断面相应于该应力状态时的 CT 图和当时测得的断面 上有关点的 CT 数。根据加载装置所获得的全过程曲 图 28 扫描断面定位线示意图 Fig. 28 Scan section position of the rock sample （2）试验条件 同步施加 σ 1 = σ 2 = σ 3 并逐步增加到 10 MPa，然 后在固定 σ 2 = σ 3 = 10 MPa 的情况下增加 σ 1 ，加载和 卸载的过程曲线见图 29。 在图 29 中用 1～7 点标示出对 4 个断面进行 CT 扫描时的应力和应变状态。第 8 点对应的是在卸载过 程进行 CT 扫描时的应力和应变状态。 岩 10 土 工 程 学 报 2008 年 图 30 南桥砂岩#5 试件各扫描断面的 CT 数取平均值与轴向应 图 29 南桥砂岩#5 试件三轴压缩荷载作用下的应力–应变关系 曲线 Fig. 30 Mean CT number of scanning sections versus axial strain Fig. 29 Stress- strain curve of Nanqiao Sandstone Specimen No. 5 subjected to triaxial compression 对 4 个断面进行 X 射线 CT 实时扫描时的应力– 应变状态见表 2。 表 2 南桥砂岩#5 试件 X 光 CT 实时扫描的应力–应变状态 Table 2 Stress-strain state of real-time CT scanning of Nanqiao sandstone specimen No. 5 扫描 次序 1 2 3 4 5 6 7 8 变的关系曲线 σ1 /MPa 11.88 22.63 35.92 45.66 48.85 49.47 51.71 40.79 (σ1-σ3) /MPa 1.88 12.63 25.92 35.66 38.85 39.47 41.71 30.79 ε /‰ 0.63 2.5 5.0 6.9 7.6 7.9 8.5 11.6 备注 门槛值 （3）南桥砂岩#5 试件的试验结果 对#5 试件 4 个断面 8 次扫描所得 CT 数列在表 3。 # 5 试件 4 个断面的 CT 数的平均值与#5 试件的轴向应 变的关系如图 30 所示。 curve of Nanqiao sandstone specimen No. 5 南桥砂岩#5 试件加载过程的 4 个扫描平面的 CT 图 见图 31（a）～（g） 。南桥砂岩#5 试件卸载到 σ 1 =40.79 MPa 时的 4 个扫描断面的 CT 图像见图 31（h） 。 # 2.4 南桥砂岩 5 试件试验结果与应力-应变全过程曲 线的关系 从图 32 可以看出#5 试件实测的全过程曲线（图 32（a） ）与传统的岩石全过程曲线（图 32（b） ）的规 律是一致的。结合图 30，也可看出 CT 数的变化规律。 （1）图 32（b）中的 OA 段即 σ 1 从 11.88 MPa（#1 点）增加到 22.63 MPa（#2 点）的区段是初始的微裂 隙有所压密，因此。密度有所增加，从而 CT 数也有 所增加。 （2）在第二阶段期间在图 32（b）上即 AB 段。 此时，σ 1 由 22.63 MPa（#2 点）增加到 35.92 MPa（#3 点） 。在此阶段内 CT 相对保持不变其均差也没有多少 变化，因为此段是岩石的的弹性阶段。σ 1 达到 36 MPa 时似乎就是一个门槛值。此过点后就是非线性阶段的 开始。 图 31 三轴压缩荷载作用下南桥砂岩#5 试件各层面 CT 图像 Fig. 31 CT Images of four sections of Nanqiao sandstone specimen No. 5 subjected to triaxial compression 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 11 表 3 三轴压缩荷载作用下南桥砂岩#5 试件 4 个 CT 扫描层在不同应力水平下的实验数据 Table 3 Testing result of 4 CT scanning sections at different stress level of Nanqiao sandstone specimen No. 5 subjected to triaxial compression 扫描 序次 1 2 3 4 5 6 7 8 第 1 扫描层 CT 数 方差 1625.6 98.95 1626.6 104.52 1627.6 105.50 1626.6 105.63 1625.9 104.35 1624.5 101.54 1622.9 97.53 1609.9 91.56 第 2 扫描层 CT 数 方差 1630.0 102.07 1633.6 104.51 1634.3 104.74 1634.2 102.19 1632.0 101.07 1627.4 100.71 1621.5 99.87 1604.3 113.37 第 3 扫描层 CT 数 方差 1592.6 105.01 1598.2 105.10 1601.1 104.94 1602.3 104.07 1601.9 101.05 1596.7 97.11 1591.0 98.84 1576.9 115.51 第 4 扫描层 CT 数 方差 1582.3 172.03 1583.5 172.86 1584.5 166.57 1585.2 166.76 1584.8 166.67 1581.5 165.44 1578.7 165.74 1565.4 183.29 图 33 第一扫描层面损伤发展与裂面的发展 Fig. 33 Damage and fissure evolution at the first scanning section 图 32 实测应力–应变全过程曲线与典型曲线对比 Fig. 32 Comparison of Stress-stain whole process curve obtained from testing to the classic one （3）第三阶段 BC 段已是非线性阶段，即图 31 （a）中的#3 点到#5 点的阶段但变化还十分微弱。但 当 σ 1 增加到 49 MPa 左右时（#5 点）开始了非常激烈 的变化。 （4）据此开始 CD 段，即包括#5、#6、#7 点和峰 值强度点在内的阶段，就是裂隙激烈扩展阶段，而且 形成了大的裂缝，当达到了峰值强度 53.12 MPa 时， 大的裂缝贯穿了整个试件，CT 数急剧下降。 （5）最后阶段即图中的 DE 段，即从峰值强度点 # 到 8 点，是峰后段，损伤发展极为快速，当卸载到 σ 1 =40.79 MPa 时（#8 点），已经出现了数条重要的贯 穿裂缝并且快速张开，整个试件的体积处于膨胀状态 而频临崩溃。 上述 5 个阶段的状态，可用图 33 即第一扫描层面 的 CT 图来展示损伤发展与裂面的发展情况。 3 关于边坡与坝基抗滑稳定分析的一 种新方法——矢量和分析方法 3.1 抗滑稳定分析方法的进展 近年来随着有限元方法等的普及，在边坡与坝基 抗滑稳定分析中采用有限元分析已日益普遍[22-25]。从 1927 年 Fellenius[26]提出边坡稳定分析的早期条分法， 经过 80 a 的发展， 极限平衡分析法已取得长足的进步。 瑞典法是建立在圆弧滑动面基础上的，而且又是孤立 条块，条块间不传力，潜在滑动面上采用莫尔–库仑 强度准则，因此抗滑稳定安全系数为 n ∑ (σ f + c ) ∆l K = i =1 i i i n ∑ τ ∆l i =1 i i ， (6) i 式中， σ i ， τ i 分别为作用在圆弧状滑动面第 i 段的平 均法向应力（压为正）和平均剪应力， ∆li 为第 i 段的 段长， fi 和 ci 分别为第 i 段的抗滑摩擦系数和粘结力， n 为圆弧状滑动面的分段总数。 这个以代数和描述的安全系数计算公式相对于圆 弧状滑动面来说是合理的，因为式（6）满足了力矩平 衡原理，代数和能够成立。对于沿一个平面发生滑动 的情况，式（6）也可以成立。 在通常情况下，潜在滑动面并非圆弧状，它可由 多个直线段组成的折线状，也可是任意的曲线。条块 间的作用力不能忽略，条块间作用力的分布特点即作 用点位置和作用力的方向可有不同的假设。作用在坡 体的荷载也是复杂的，例如有地下水的作用，有地震 12 岩 土 的作用，还有其它类型的荷载作用在坡体表面和坡体 内。这些因素促使了极限平衡条分法有了很大发展。 众所周知，坡体作用在滑动面上的应力分布，由于是 一个超静定问题，不作什么假定是难以算出来的。极 限平衡条分法这数十年来的发展可以说是环绕着对条 块划分的方式，对条块界面上作用力的大小、方向和 作用点的种种不同的假定，以及安全系数的评定方式 等形成了多种著名的方法可参阅文献[27]。其中 Sarma 法是以其斜分条块为其特色的。 湖北省大冶铁矿露天采矿场南邦边坡稳定研究 （1964 年～1967 年） 是我国早期最具标志性的岩质边 坡稳定性研究课题。在陈宗基先生领导下曾开展了大 量的工程地质勘测工作和岩体力学现场试验。在这项 研究课题中笔者曾提出了空间五面体抗滑稳定计算分 析公式和考虑开挖爆破影响的平面问题极限平衡分析 方法，也采用过不用强度储备概念，也不用迭代过程， 只作一次计算在最后一个条块外界面上作用有“剩余 推力或拉力”，一次求出抗滑稳定安全系数[28]。1980 年潘家铮发表了大坝坝基与边坡的极限平衡分析法专 著[29]，陈祖煜不但总结了国际上一些著名的边坡分析 方法，还对许多方法作了很大的改进[27]。 极限平衡稳定分析方法在我国近年来已从二维向 三维扩展，并有了良好的进展。更可喜的是，最近又 有了三维准严格极限平衡法和“无条分”的极限平衡 分析法和严格三维平衡法面世[30-32]，但采用的还是基 于强度储备概念的安全系数。 在抗滑稳定的安全度量上有两大范畴：①确定性 的，即采用安全系数的概念；②考虑非确定性因数的 边坡可靠性分析。文献[33]是边坡可靠性分析有代表 性的著作之一，有关可靠性分析不属本文探讨范围。 3.2 关于强度储备安全系数的讨论 （1） c ， ϕ 值取同样的折减系数不很合理 众所周知，在采用莫尔–库仑强度准则时，c ，ϕ 是抗剪强度的两个参数，它们在强度准则中所起的作 用不相同，力学属性也不同。特别是对岩石介质而言， 不同岩性的 c 值变动范围非常大，从测定方法来说此 值也是很难测得准，同一岩性的多次测定结果的波动 范围也很大。而 ϕ 值则不然，工程中遇到的边坡有不 同类型，有的在保持它们稳定性方面 c 值起重大作用， 有的 c 值不起多少作用而是 ϕ 值起关键作用。因此， 对于采用统一的强度折减系数 F 作为安全系数，实际 上对于不同性质的边坡其安全裕度内涵是不一样的。 如果将两者除以不同的值，即 Fc 和 Fϕ ，那么问题就复 杂化了，将得到无穷多的 Fc 和 Fϕ 的组合解。如果固定 一个参数不变，即变动另一个参数，那么也有两个解 答，即 Fϕ（ c 等于原值不变）和 Fc（ ϕ 等于原值不变） ， 工 程 学 报 2008 年 这也就不再能成为安全系数的定义。 （2）当潜在滑动面切过性质不同的介质时，这些 介质的 c ， ϕ 值很不相同，此时还是用统一的强度折 减系数 F 作为边坡的安全系数更是十分勉强的。 （3）第三个问题实际上是个理论问题。如果采用 莫尔–库仑强度理论， ϕ 值的取值是有条件的。郑宏 等[24]已经证明，在对强度参数进行折减的同时必须对 泊松比 µ 也要作相应调整使满足 (7) sin ϕ ≥ 1 − 2 µ ， 这样才能得到合理的分析结果。由此可见，在做有限 元分析并以强度折减系数作为安全系数值时，在许多 情况下 µ 值也需作适当调整以满足上述的不等式。如 果调整 ϕ 值时，也调整了 µ 值，那么这个安全系数将 不成为其原先定义的强度储备型安全系数了。如果不 调整 µ ，即不满足前述的不等式，结果将是不合理的。 （4）强度折减后得到的坡体和潜在滑动面上的力 学状态并不是一个真实的状态， 它只是某种虚拟状态。 我们认为比较合适的途径应该是从它的当前的真实力 学状态出发，不用迭代过程，就能一次计算得出它的 安全系数的办法来。从道理上讲，以它的真实状态出 发得到的结果更为合理，也更为直接。 （5）用有限元分析时对岩土介质要实施强度折减 的范围如何确定？由于强度折减的影响往往会引起在 不应该出现塑性区或破损区的部位出现这些区域。这 些区域的出现会或多或少影响整体的状态，从而也会 对据此得出安全系数值和合理性有一定影响。 （6）采用强度折减 F 值时，当总体很接近极限 平衡时，此时有限元的求解将十分困难，常常难收敛， 因此产生了一个如何判断是否已处于极限状态时的综 合评判问题。另外这种非线性计算与选取的本构模型、 强度判别准则等都有很大关系。举例来说，如采用 D-P 准则，那又要区分采用外接圆或内接圆或“等面积” 圆，结果将各不相同，直接采用莫尔–库仑的结果则 显然与 D-P 的也不相同，如果后者采用角部圆化处理 也将不相同。不同的人采用不同本构和强度准则得到 的安全系数也必然不同。这就对这种强度储备型的抗 滑稳定安全系数的可靠性和合理性带来了问题。 3.3 抗滑稳定安全系数“矢量和”分析方法的提出及 基本概念 边坡与坝基抗滑稳定分析方法都是在对“潜在” 滑动体和“潜在”滑动面进行受力分析的基础上定义 和求解抗滑安全系数，根据安全系数的大小来判定其 稳定程度。 笔者认为，最经典抗滑稳定安全系数 K 的概念和 定义应该是：坡体在受各种荷载（包括自重）作用条 件下，潜在滑动面所能提供的极限抗滑力的“总和” 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 与作用在潜在滑动面上滑动力的“总和”之比。这样 的定义是非常直观和朴实的。我们提出的“矢量和” 分析法基于如下 5 点。 （1）这里说的“总和”，并不是力的简单叠加， 因为力是矢量。把作用在潜在滑动面上各分段的滑动 力矢量按“矢量和”合成为导致坡体可能发生滑动的 力矢，称之为总滑动力矢。同理，把作用在潜在滑动 面上各分段的抵抗滑动的力矢，通过“矢量和”形成 总抗滑力矢。 （2）因为总抗滑力矢与总滑动力矢都是矢量，不 可能通过直接对比形成用标量表达的抗滑稳定安全系 数。它们必须在某一方向上进行投影才能计算出具有 标量性质的抗滑稳定安全系数 K 。 （3）向不同方向投影所得的结果是不同的。因此， 要确定最合理，而且有明确物理含义的投影轴。 （4）在二维状态下总滑动力矢与总抗滑力矢在一 个平面内。作用在潜在滑面上各段的剪力 τ i ∆li 的矢量 和的方向代表坡体可能发生滑动的趋势方向，称之为 坡体滑动趋势方向。经过多年研究我们认为将坡体潜 在滑动方向作为投影轴是合理的。本文将以这样的投 影轴作为分析基础。我们也研究了以潜在滑动面的法 向力引起总抗滑力矢作为投影轴也是可取的，其分析 结果与前者相差非常小。 （5）在三维状态下采用同样的原则，将潜在滑动 面上各微元面上滑动力通过“矢量和”合成总滑动力 矢。将滑动面上各微元面 δ i 上的 τ iδ i 合成的矢量方向 称为整体滑动方向。各微元面上的抗滑力通过“矢量 和”合成总抗滑力矢。将总滑动力矢与总抗滑力矢向 坡体潜在滑动方向投影，它们的比值称之为“矢量和 法”抗滑稳定安全系数。 上述 5 点构成了“矢量和法”抗滑稳定安全系数 计算法的基础。 1983 年在全国水工建筑物复杂地基非线性有限 元程序讨论会上笔者首次提出“矢量和”分析方法的 概念和初步设想。后又对“矢量和”法做过一些改进 [23-35] ，又与其它方法的结果作了比较[36-37]。 “矢量和” 法是一个广义的方法，它既适用于有限元分析也适用 于极限平衡条分法。 3.4 边坡与坝基抗滑稳定问题的矢量和分析方法 （1）平面问题的矢量和分析法 各种边坡与坝基抗滑稳定分析方法都是在对潜在 滑动坡体进行受力分析的基础上，在潜在滑动面上定 义和求解抗滑稳定安全系数： ∑R ， K= (8) ∑T 13 式中，∑ R 为潜在滑动面上总的抗滑能力，∑ T 为总 的下滑能力。 由于抗滑力与下滑力都是矢量，所以式（7）中对 抗滑力与下滑力的求和都应是矢量的求和。为此，我 们提出矢量和分析法，将安全系数 K 的定义建立在力 的矢量分析基础上， 并将其称为 “矢量和法安全系数”。 （2）矢量和分析法的基本假定与原则 a）以二维问题为研究对象，边坡或坝基所构成的 计算区域为Ω，在Ω内的潜在滑动面 L 已知，构成的滑 动区域为 S，本文不探讨搜索最危险滑动面的方法。 实际工程中，对于某一具体的边坡或坝基，特别是岩 质边坡和岩基，进行稳定分析的前提条件就是通过地 质勘察，获得各潜在滑动面的空间形态及滑体、滑带、 滑床等要素的物理力学参数[38]。 b）边坡与坝基的荷载、边界条件、岩土体的基本 物理力学参数已通过勘察获得，用有限元法等数值方 法可计算出边坡与坝基内的应力分布状况。 c）滑动面上岩土体的强度特性服从莫尔–库仑强 度准则。在应力分布已知时，岩土体的抗剪强度为 τ f = c + σ tan ϕ 。 (9) d）以边坡与坝基的整体抗滑稳定性为研究目的， 安全系数的计算方向由边坡与坝基的整体滑动趋势确 定。文中具体来说以作用在潜在滑动面由 τ i ∆li 形成的 分段剪力，通过“矢量和” ，形成总力矢，其方向为计 算方向 θ ，即滑动力矢和抗滑力矢投影方向。 e）矢量和法安全系数 K (θ ) 定义为，沿计算方向 θ ，滑动面上提供抗滑力的各力沿此方向投影的代数 和 ∑ R (θ ) 与提供滑动力的各力沿此方向投影的代数 和 ∑ T (θ ) 比值： ∑ R (θ ) 。 K (θ ) = (10) ∑ T (θ ) （3）平面问题矢量和法抗滑稳定性安全系数计算 方向 θ 的算式 如图 34 所示，假定在边坡与坝基的荷载、边界条 件、滑动面位置、岩土体的基本物理力学参数已知的 情况下，用有限元法计算的潜在滑动面上任意一点 i 处在其局部坐标系 X ′O′Y ′ 下的应力为 σ i 和 τ i ， i 处的 一微弧段为 ∆li ，点 i 处滑动面的切线与总体坐标系 X 轴正向的夹角为 α i 。 应力的正负号按岩土力学的规定。角度的正负规 定为：从 X 轴正向出发沿逆时针方向的角度为正，沿 顺时针方向的角度为负，图 34 中的 α i 为负。 根据摩擦理论，边坡与坝基的潜在滑动面上的任 意一点 i 的滑动剪力方向应沿着该点的滑动面的切向 方向，因此该点的应力在滑动面切向方向的分量 τ i 与 岩 14 土 ∆li 的乘积就是该点处促使坡体滑动的剪力大小，而 对于整个滑体，潜在滑动面各段的下滑力的合力矢就 是整个滑体的潜在滑动趋势方向。而矢量和法安全系 数的计算方向就是滑体的整体潜在滑动趋势方向。 图 34 确定计算方向θ Fig. 34 Determination of calculating direction θ τ i ∆li 在 X 方向的投影 Fxi = τ i ∆li cos α i ； (11) τ i ∆li 在 Y 方向的投影 Fyi = τ i ∆li sin α i 。 (12) 所以，计算方向 θ （即滑体的整体滑动趋势方向）为 θ = arctan ∑F ∑F yi 。 (13) xi （4）矢量和法安全系数的求解表达式 图 35 为边坡抗滑稳定分析“矢量和”法的安全系 数计算示意图。以潜在滑动面为研究对象，在滑动面 上某一点 i 处，岩土体的黏聚力为 ci，内摩擦角为 ϕi ， 滑体作用于基岩潜在滑动面上的荷载为正应力 σ i 和 剪应力 τ i ，基岩作用在潜在滑动体上的反力为 σ i′ 和 τ i′ ，它们相互之间分别构成作用力与反作用力，即 σ i′ = σ i ， τ i′ = τ i 。 (14) 安全系数计算方向和滑动面切线与 X 轴正向的夹角分 别为 θ 和 α i ， θ 由式（13）确定。 图 35 “矢量和”法安全系数求解示意图 Fig. 35 Diagram of solving the vector sum safety factor 推导式（10）的过程分析如下。 a）滑动面上的滑动力由外部荷载和自重引起，在 滑动面的一个微段 ∆li 内，就是由滑动面上该处的 σ i ， 工 程 学 报 2008 年 τ i 引起，将各种引起滑动力的力沿安全系数计算方向 θ 进行投影，并应用式（14），然后求和即为式（10） 中的分母项。 τ i ∆li 的投影为 Tτi = τ i ∆li cos (θ − α i ) ； (15) σ i ∆li 的投影为 Tσi = σ i ∆li sin (θ − α i ) 。 (16) 所以 (17) ∑ T (θ ) = ∑ Tτi + ∑ Tσi 。 b）潜在滑动面上的抗滑力由岩土体的黏聚力、摩 擦力及基岩对滑动面的法向反力提供；滑动面的一个 微段 ∆li 内，黏聚力与摩擦力之和就是滑动面岩土体的 抗剪强度 τ fi ，其值由莫尔–库仑强度准则计算，基岩 对滑动面的法向反力为 σ i′ （ = σ i ） 。 τ fi = ci + σ i tan ϕi 。 (18) τ fi ∆li 的投影为 Rτi = τ fi ∆li cos (θ − α i ) ； (19) σ i′∆li （= σ i ∆li ）的投影为 Rσi = σ i ∆li sin (θ − α i ) 。 (20) 所以 ∑ R (θ ) = ∑ Rτi + ∑ Rσi 。 (21) c）将式（17）、（21）代入式（10），得矢量和法 安全系数的表达式： ∑ R (θ ) = ∑ Rτi + ∑ Rσi 。 K (θ ) = (22) ∑ T (θ ) ∑ Tτi + ∑ Tσi 抗滑稳定安全系数 K = K (θ ) ，并将式（18）代入 式（22）展开得： n ∑ ⎡⎣( c + σ f ) cos (θ − α ) + σ sin (θ − α )⎤⎦ ∆l K = K (θ ) = i =1 i n i i i i i ∑ ⎡⎣τ i cos (θ − α i ) + σ i sin (θ − α i )⎤⎦ ∆li i ， i =1 (23) 当 σ i 为拉应力时，可令该微面提供的摩阻力为 0。 3.5 矢量和法抗滑稳定安全系数的计算步骤 根据前述矢量和法安全系数定义表达式的理论推 导，矢量和分析法的抗滑稳定安全系数的主要计算步 骤如下：①根据地质勘察资料建立有限元数值计算模 型，在模型中根据地质勘察等资料定出潜在滑动面； ②对模型进行常规的有限元弹（塑）性分析计算，得 到潜在滑动面上各点的应力状态；③通常按有限元网 格划分的结点，将滑面分为若干个小段进行计算，根 据有限元弹（塑）性计算结果，计算潜在滑动面上各 处剪应力与微段 ∆li 的乘积可求得总力矢，按本文前述 的约定可将该总力矢的方向即为安全系数的计算方 向；④在安全系数的计算投影方向上按式（17） 、 （21） 计算滑面上各处微段滑动力与抗滑力沿此方向投影的 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 代数和，按式（23）就可得到边坡或坝基整体的安全 系数，根据安全系数大小来分析和判断边坡或坝基的 整体稳定性。 3.6 采用极限平衡条分法时的计算方法 按 c ， ϕ 的实际取用值计算。由于条分不同和处 理条块间相互作用力方式不同，可以有不同的假定。 只需作一次计算都可得到潜在滑动面上的各 ∆li 段上 的滑动力和抗滑力。但此时坡体在一般情况下并不处 于极限平衡状态，只在最后一个条块的外界面上作用 → 有一个拉力，或压力矢量 A 才能使总体处于极限平衡 状态。此时，将各 ∆li 段上的滑动力矢量合成总滑动力 矢量，将各 ∆li 段上的抗滑力矢量合成总阻力矢量，然 后按式（13）和（23）可求出抗滑稳定安全系数值。 值得注意的是，这样做不需要迭代过程，也不需要采 → 用强度储备的概念。当 A 矢量指向最后一个条块的外 界面时意味着坡体需要有增加的抗滑力才能保持极限 → 平衡， A 的量也可作为计算必需增加抗滑力的基础。 3.7 ACADS 两道边坡考题算例与“矢量和”分析结 果的对比分析 从 1987 年澳大利亚计算机应用协会（ACADS）。 考题 1 中的 EX1（a）和 EX1（c）为例来说明[23]。 考题 EX1（a）为一均质土坡，其计算模型及尺 寸如图 36 所示。考题 EX1（c）为非均质土坡，其轮 廓尺寸与 EX1（a）相同，但坡体由 3 种土层组成， 计算模型及尺寸如图 37 所示。 图 36 ACDAS 考题 EX1（a）计算模型 Fig. 36 Calculating model of ACDAS 本文不讨论边坡与坝基抗滑稳定矢量和分析法的 临界滑动面的搜索问题，图 36，37 中的滑动面为文献 15 [23]采用 STAB 程序求得的临界滑动面，本算例即以 此滑动面进行边坡稳定分析的计算，考题 EX1（c） 的滑动面同时穿过 3 种土层。 图 37 ACDAS 考题 EX1（c）计算模型 Fig. 37 Calculating model of ACDAS 我们基于大型有限元商用软件 ANSYS 的二次开 发，运用边坡与坝基稳定的矢量和分析法，为两道考 题算例编写了相应的求解矢量和法抗滑稳定安全系数 的计算程序。各种方法计算结果请参看表 4。 通过对表 4 中各种分析方法所得到的安全系数的 对比分析可知，运用本文提出的分析方法对两个标准 考题计算的结果与依据极限平衡法得到的各裁判答案 非常接近，考题 EX1（a）和考题 EX1（c）运用本文 提出的方法的计算结果与推荐的 Donald 的裁判答案 相比，其相对误差分别只有 1.06%和 0.43%。 对于这两个算例，我们还运用有限元强度折减法 对其稳定性进行了分析，分析时以计算不收敛作为破 坏 标 准 ， 屈 服 准 则 为 Druker-Prager 准 则 （Mohr-Coulomb 准则的外接圆） 。考题 EX1（a）和 EX1（c）的有限元强度折减安全系数分别为 1.188 和 1.578，比裁判答案分别高出了 18.75%和 13.53%，由 于采用了外接圆可能是原因之一。 3.8 非圆弧滑动面边坡稳定安全系数的“矢量和”法 分析 （1）计算模型 为了进一步考察本章提出的边坡与坝基抗滑稳定 分析方法的一些特点，本节选取的滑动面形状有：单 直线、双折线、三折线、任意曲线等 4 种。各模型的 材料参数、外形尺寸和边界条件与前节 ACADS 的标 表 4 ACADS 两道考题的裁判答案与各种计算方法所得结果的对照表 Table 4 Comparisons of safety factors for ACADS with different calculating methods 分析方法 极限平衡法裁判答案 有限元强度折减法 本文方法 计算程序名 Donald(推荐) SSA(Baker) STAB(Chen) GWEDGEM EMU Fredlund ANSYS ANSYS(弹性应力) 安全系数 1.000 1.000 0.991 1.000 1.000 0.990 1.188 1.011 EX1(a) “矢量和”法 F(θ) -21.82 安全系数 F(θ) 1.390 1.390 1.385 1.390 1.390 1.406 1.578 1.384 EX1(c) “矢量和”法 F(θ) -21.51 岩 16 土 准考题 EX1（a）相同，各计算模型及其单元划分见 图 38，这些图中也标明了滑动面的具体形状与位置。 图 38 4 种非圆弧型滑动面 Fig. 38 Four kinds of non-circular slip surface （2） “矢量和”法计算结果与其它方法结果的对 比分析 工 程 学 报 2008 年 各滑动面运用矢量和分析法计算的矢量和法安全 系数如表 5 所示，表中同时列出了运用极限平衡法对 这些滑动面进行计算所得到的安全系数。 极限平衡法的计算软件是 GEO-SLOPE Office5， 表中的 M-P 法指的是 Morgenstern-Price 法，L-K 法指 的是 Low-Karafiath 法。分析表中的数据可知，3 种极 限平衡方法在单直线滑动面情况下的计算结果与本文 方法的矢量和法安全系数相差很小，相对误差都没有 超过 1%。在其它几种滑动面情况下，本文方法的矢 量和法安全系数与极限平衡法中的 Morgenstern-Price 法和 L-K 法的计算结果有一定的差别，与这两种方法 计算的安全系数最多相差分别为 2.483%和 2.190%； 本文方法的矢量和法安全系数与 Bishop 法的计算结 果在三折线滑动面的情况下相差达到了 5.631%，且 Bishop 法计算的安全系数除单直线滑动面外，其它几 种滑动面情况下的计算结果比表中所列的其它方法计 算的结果都要高，这主要是因为 Bishop 法是基于圆弧 滑动面的分析方法。 3.9 有关矢量和分析方法的讨论 （1）有限元网格单元尺寸大小对矢量和分析方法 得出的 K(θ)的影响 我们以三折线滑动作为算例，采用不同单元尺寸 进行剖分，并采用弹性计算所得出的计算方向θ和抗 滑稳定安全系数见表 6。算例表明，单元尺寸大小对 K(θ)影响不大，对θ角的影响也较小。单元尺寸大时的 K(θ)稍大于单元尺寸很小的 K(θ)，但两者的相对差值 仅 1.10%。 本算例的 K(θ)与单元尺寸关系曲线见图 39。 表 5 采用各类不同方法求解的沿各类滑动面的边坡稳定稳定系数与“矢量和”法的结果对比表 Table 5 Comparison of safety factors from vector sum method and other methods according to the different slip surfaces 计算模型滑动面 单直线 双折线 三折线 任意曲线 M-P 法 1.684 1.071 1.097 1.047 极限平衡法安全系数 Bishop 法 L-K 法 1.678 1.682 1.139 1.076 1.163 1.106 1.116 1.050 安全系数 K(θ) 1.668 1.091 1.101 1.073 本文方法：有限元弹性 计算方向θ/(°) 单元数 4274 -18.43 2195 -20.96 2199 -20.00 2338 -20.45 节点数 4447 2324 2328 2467 表 6 单元尺寸对“矢量和”法安全系数的影响 Table 6 The impact of element scale on vector sum safety factor 单元尺寸/m 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 单元数量 642 844 1107 1471 2085 3423 5902 13433 49986 注：表中的相对误差是以 0.1 m 的为基础。 安全系数 K(θ) 1.1116 1.1086 1.1060 1.1033 1.1027 1.1011 1.1005 1.1012 1.0997 相对误差/% 1.10 0.83 0.59 0.35 0.29 0.15 0.09 0.15 0.00 计算方向θ/(°) -20.05 -20.10 -20.04 -20.04 -19.98 -20.03 -20.03 -19.96 -19.938 相对误差/% 0.56 0.81 0.51 0.51 0.21 0.46 0.46 0.11 0.00 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 图 39 安全系数随单元尺寸的变化 Fig. 39 Variations of safety factor with element scales （2）矢量和抗滑稳定分析法中采用弹性应力状态 和弹塑性应力状态对 K(θ)的影响 为了考察弹性应力状态和弹塑性应力状态对安全 系数的影响，分别对上述算例进行了这两种应力状态 下的安全系数，如表 7 所示。其中塑性本构用 D-P 准 则，分别取莫尔–库仑准则的外解圆和内接圆，显然 莫尔–库仑介于二者之间。 可以看出，塑性应力状态下的安全系数比弹性应 力状态下的稍小一点，这两种应力状态下的安全系数 相差很小，仅在小数点后第二位有所变化，这点也很 容易理解，弹塑性应力状态只不过是在弹性应力状态 基础上对不满足剪切强度准则部分的剪应力向周围区 域转移的结果，这种调整主要是调整剪应力的大小和 位置，其合力矢方向没有大的变动，整体的滑动力矢 的长度没有很大的变化，结果是弹性应力状态或弹塑 性应力状态对“矢量和”边坡稳定安全系数影响很小。 在大多数情况下用弹性应力状态来计算安全系数 足以满足工程精度要求。 （3）关于投影方向角等问题的讨论 投影方向角的选择是可以作更深入的研究。总的 原则是以潜在滑动面的滑动趋势为原则，本文假定的 总滑力矢为投影方向。实际上也可用总抗滑力矢或平 均滑动方向为投影方向。我们曾作过详细比较，三者 所得的结果相差甚微，基本一致。选择后两种可能更 有利于滑动面的自动搜索。 3.10 三维“矢量和”边坡稳定安全系数法公式 17 式，这里采用弹性力学拉正压负的约定。 对于滑面上任一点，微面 dA 其法线方向为 n ，这 里规定指向滑体内部为正向，应力状态为 σ ，如图 40 所示，则该面上的应力分量为 σa = σ ⋅ n ， (24) 与平面垂直的应力分量为 σn = ( σ ⋅ n ⋅ n) n = σn n ， (25) 切向分量为 στ = σ a − σ n ， (26) 整体潜在下滑方向为 r = ∫ στ dA ， A (27) 潜在滑面上局部单位剪切应力方向为 σ στ0 = τ ， στ (28) 则安全系数表达为 ∫ ⎡⎣( c − σ f ) στ + σ ⎤⎦dA ⋅ r 。 K= ∫ σ dA ⋅ r 0 A n A n (29) a 需要注意的是，因为边坡或坝基一般处于受压状态， 故式（29）中 σ n 大多数为负值。在法向应力 σ n ≥ 0 时， 可令式（29）的 c = f = 0 。 图 40 坡体潜在滑面受力示意图 Fig. 40 Diagram of forces acting on a slop slip surface 3.11 几点结论 （1）在使用计算机近代数值分析方法未普及之 前，人们很难摸清边坡或坝基内部应力场的精确分布 情况，传统边坡或坝基安全系数的计算是在强度储备 意义下通过极限平衡法来实现是有其历史原因的。 为了方便推导三维矢量和边坡稳定性安全系数公 表 7 采用不同本构求解的沿各类滑动面的边坡稳定“矢量和”法稳定系数 Table 7 Vector safety factors from the slip surfaces with different constitutive equations 弹性 计算 模型 单元数 节点数 单直线 双折线 三折线 任意曲线 4274 2195 2199 2338 4447 2324 2328 2467 安全系数 K(θ) 1.668 1.091 1.101 1.073 注：剪胀角取 0°；”—”代表弹塑性分析不收敛。 计算方向 θ/(°) -18.43 -20.96 -20.00 -20.45 弹塑性 (D-P 外接圆) 计算方向 安全系数 θ/(°) K(θ) 1.666 -18.43 1.086 -21.16 1.100 -20.33 1.067 -21.01 弹塑性 (D-P 内接圆) 计算方向 安全系数 θ/(°) K(θ) 1.665 -18.43 — — — — — — 岩 18 土 （2）随着人们计算能力的提高，得到计算区域的 当前真实的应力状态已不成问题。本文就是在此基础 上，依据经典安全系数的概念，根据真实的应力状态 提出了将总抗滑力矢和总滑动力矢在潜在滑动方向上 投影之比作为安全系数。 （3）在此基础上提出了适用于边坡和坝基抗滑稳 定分析的一种新方法——矢量和分析方法。 （4）本文比较了矢量和法与传统方法之间的关 系， 表明了矢量和法求解抗滑稳定安全系数的合理性。 （5）此方法具有如下优点：①因为力是矢量，这 使得投影的物理意义更加准确；②矢量和法抗滑稳定 安全系数公式是显式表达式，不需要迭代求解，不存 在收敛性问题；③对于有限元法或极限平衡条分法， 矢量和抗滑稳定分析法都可适用；④用有限元求得应 力场后，再用矢量和方法得到的安全系数，该安全系 数对单元划分尺寸并不敏感；⑤用有限元法在弹性应 力状态或弹塑性应力状态下得到的应力场对结果影响 较小；⑥公式简洁，物理意义明确，且容易编制程序， 容易被工程技术人员掌握和应用。 （6）与传统极限平衡意义下得到的安全系数比较 可以看出，现有的安全系数许用准则，也应该同样可 以适用于边坡与大坝坝基抗滑稳定矢量和分析方法。 4 结 论 （1）大量试验揭示了这样的规律，即岩石发生疲 劳破坏时受它应力–应变全过程曲线所控制。 （2）岩石疲劳破坏受应力–应变全过程线控制规 律对于沉积岩类，变质岩类和火成岩类是普适的。 （3）岩石疲劳破坏受应力–应变全过程线控制这 一重要试验结果提示我们研究岩石问题时要十分重视 不可逆变形的积累问题。从变形角度研究强度理论是 十分重要的方向。 （4）与岩土力学室内试验同步进行的实时 X 射 线 CT 扫描是岩土力学试验方面值得重视的一项新技 术， 为了解岩土力学破坏过程提供了一种直观的手段。 （5）基于细观层次的新的试验技术能为损伤理论 的发展和岩土力学宏观性质的解释提供新的手段。 （6）实时 X 射线 CT 扫描三维成像和许多现象的 解释工作是今后研究和发展的重点。 （7）坝基与边坡抗滑稳定的分析方法是相对“古 老”，但仍然是十分重要的与工程建设关系密切的课 题。 （8）现在普遍使用的方法，特别是用强度储备概 念去定义安全系数存在许多值得商榷的问题。 （9）矢量和分析方法是一种新方法，基于力是矢 工 程 学 报 2008 年 量的概念，观点明确和清晰。文中给出算例并与传统 方法作了对比，证明此方法是合理的。 （10）由于矢量和分析方法是一种新方法值得进 一步研究、发展和推广。 致 谢：写作过程中得到李春光博士、任建喜博士、刘艳章博 士、侯明勋博士、孙红博士、蒋宇硕士和卢允德硕士的帮助， 在此深表谢意。 参考文献： [1] WAWERSIK W R, FAIRHURST C. A study of brittle rock fracture in laboratory compression experiments[J]. Int Rock Mech and Min Sci & Geomech Abstr, 1970, 7(5). [2] 葛修润, 周伯海, 刘明贵. 电液伺服自适应控制岩石力学 试验机及其对岩石力学某些问题研究的意义[J]. 岩土力学, 1992, 13(2): 8 – 13. (GE Xiu-run, ZHOU Bai-hai, LIU Ming-gui, et al. The servo-controlled rock mechanics testing machine based on the self-adaptable principle and its significance for some research field of rock mechanics[J]. Rock and Soil Mechanics, 1992, 13(2): 8–13. (in Chinese)) [3] 葛修润, 周伯海, 刘明贵. 电液伺服自适应控制岩石力学 试验机及其对岩石力学某些问题研究的意义[J]. 岩土力学, 1992, 13(3): 8 – 13. (GE Xiu-run, ZHOU Bai-hai, LIU Ming-gui, et al. The servo-controlled rock mechanics testing machine based on the self-adaptable principle and its significance for some research field of rock mechanics[J]. Rock and Soil Mechanics, 1992, 13(3): 8–13. (in Chinese)) [4] 葛修润, 周伯海. 岩石力学室内实验装置的新进展—— RMT-64 岩石力学试验系统[J]. 岩土力学, 1994, 15(1). (GE Xiu-run, ZHOU Bai-hai. The new progress in rock mechanics testing equipment at lab—RMT-64 rock mechanics testing system[J]. Rock and Soil Mechanics, 1994, 15(1): 50–56. (in Chinese)) [5] 葛修润, 周伯海, 刘明贵, 等. 计算机方法在岩石力学中的 应用[M]//计算机方法在岩石力学中的应用. 武汉: 武汉测 绘科技大学出版社, 1994: 502–507. (GE Xiu-run, ZHOU Bai-hai, LIU Ming-gui, et al. Researches on post-failure behavior of rock and its numerical simulation[M]// Computer methods and its applications in rock mechanic. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 1994: 502–507. (in Chinese)) [6] 郑 宏, 葛修润, 李焯芬. 脆塑性岩体的分析原理及其应 用[J]. 岩石力学与工程学报, 1997, 16(1). (ZHANG Hong, GE Xiu-run, LEE C F. Analysis principle for rock mass with brittle plasticity and its applications[J]. Chinese Journal of 第1期 葛修润. 岩石疲劳破坏的变形控制律、岩土力学试验的实时 X 射线 CT 扫描和边坡坝基抗滑稳定分析的新方法 19 Rock Mechanics and Engineering, 1997, 16(1): 8–21. (in associated with sand production suing X ray CT scan in real Chinese)) time[C]// Proceeding of 11th Congress of the International [7] 史贵才, 葛修润, 卢允德. 红砂岩应力脆性跌落系数的试 Society for Rock Mechanics, Lisbon. 2007. 验研究[J]. 常州工学院学报, 2007, 20(6). (SHI Giu-cai, GE [16] 葛修润, 任建喜, 蒲毅彬, 等. 岩石细观损演化规律的 CT Xiu-run, LU Yun-de. Research on coefficent of brittle stress 实时试验研究[J]. 中国科学 E, 2000, 30(2): 104–111. (GE drop of red sandstone[J]. Journal of Changzhou Institute of Xiu-run, REN Jian-xi, PU Yi-bin et al. Real-in time CT test Technology, 2007, 20(6). (in Chinese)) of the rock meso-damage propagation law[J]. Science in [8] 卢应发, 葛修润. 岩石损伤本构理论[J]. 岩土力学, 1990, China Ser E, 2000, 30(2): 104–111. (in Chinese)) 11(2). (LU Ying-fa, GE Xiu-ren. Damage constitutive theory [17] 任建喜, 葛修润, 蒲毅彬, 等. 岩石卸荷损伤演化机理 CT on rock[J]. Rock and Soil Mechanics. 1990, 11(2): 67–71. 实时分析初探[J]. 岩石力学与工程学报, 2000, 19(5): 697 (in Chinese)) –701. (REN Jian-xi, GR Xiu-run, PU Yi-bin, et al. Primary [9] 葛修润, 卢应发. 循环荷载作用下岩石疲劳破坏和不可逆 study on real-time CT testing on unloading damage evolution 变形问题的探讨[J]. 岩土力学, 1992, 14(3): 56–60. (GE law of rock[J]. Chinese Journal of Rock Mechanics and Xiu-ren, LU Ying-fa. Researches on rock fatigue failure and Engineering, 2000, 19(6): 697–701. (in Chinese)) irreversible deformation under cycle loading[J]. Chinese [18] 任建喜, 葛修润. 单轴压缩岩石损伤演化细观机理及其本 Jounal of Geotechnical Engineering. 1992, 14(3):56–60(in 构模型研究[J]. 岩石力学与工程学报, 2001, 20(4): 425– Chinese)) 431. (REN Jian-xi, GE Xiu-run. Study on rock meso-damage [10] 葛修润. 周期荷载作用下岩石疲劳破坏及变形发展规律 evolution law and its constitutive model under uniaxial 研究[C]// 第八次全国岩石力学与工程学术大会. 北京: compression loading[J]. Chinese Journal of Rock Mechanics 科学出版社, 2004. (GE Xiu-run. Researches on rock fatigue and Engineering, 2001, 20(4): 425–431. (in Chinese)) failure and its deformations under cycle loading[C]// Chinese [19] 任建喜. 三轴压缩岩石损伤扩展细观机理及其本构模型 Society for Rock Mechanics and Engineering, Proceedings of [J]. 煤炭学报, 2001, 26(6): 578–583. (REN Jian-xi. Rock the 8th National Conference on Rock Mechanics and meso-damage propagation law in the triaxial compression Engineering, edited by Sept. Beijing: Science Press, 2004. (in loading and its constitutive model[J]. Journal of China Coal Chinese)) Society, 2001, 26(6): 578–583. (in Chinese)) [11] 葛修润, 任建喜, 蒲毅彬, 等. 煤岩三轴细观损伤演化规 [20] 葛修润, 任建喜, 蒲毅彬. 岩石疲劳损伤扩展规律 CT 细 律的 CT 动态试验[J]. 岩石力学与工程学报, 1999, 18(5): 观分析初探[J]. 岩土工程学报, 2001, 23(2). (GE Xiu-run, 497–502. (GE Xiu-run, REN Jian-xi, PU Yibin, et al. A real REN Jian-xi, PU Yi-bin. Primary study on CT real-time time CT triaxial testing study on meso-damage evolution law testing on fatigue meso-damage propagation law of rock[J]. of coal[J]. Chinese Journal of Rock Mechanics and Chinese Journal of Geotechnical Engineering, 2001, 23(2): Engineering, 1999, 18(5): 497–502. (in Chinese)) 191–195. (in Chinese)) [12] 葛修润, 任建喜, 薄毅彬, 等. 岩土损伤力学宏细观试验 [21] GE X R, REN J X. Real time CT testing of rock damage 研究[M]. 北京: 科学出版社, 2004. (GE Xiu-run, REN evolution Jian-xi, PU Yi-bin, et al. Macro and meso testing study on Proceeding of 11th Congress of the International Society for damage mechanics of geotechnical media[M]. Beijing: Rock Mechanics, Lisbon, 2007. Science Press, 2004. (in Chinese)) [13] SANTOS J B, CAMPOS E, TAVARES A C. Real time X ray CT scan studies of sand production simulations[R]. Brazil: Rio de Janeiro, 2004. (in Portuguese) mechanism under triaxial compression[C]// [22] DUCAN J M. State of the art: Limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(7). [23] 丰定祥, 吴家秀, 葛修润. 边坡稳定性分析中几个问题的 [14] SANTOS J B. Experimental study of mechanicsms in sand 探 讨 [J]. 岩 土 工 程 学 报 , 1990, 12(3): 1 – 9. (FENG production using X Ray CT Scan[D]. Brazil: Dept of civil Ding-xiang, WU Jia-xiu, GE Xiu-run. Some Problems of Eng Catho lic University, Rio de Janeiro. 2004: 142. (in Slope Stability Analysis[J]. Chinese Jounal of Geotechnical Portuguese) Engineering, 1990, 12(3): 1–9. (in Chinese)) [15] SANTOS J B, BARROSO E V, et al. Studies of mechanicsms [24] 郑 宏, 李春光, 李焯芬, 葛修润. 求解安全系数的有限 岩 20 土 元法[J]. 岩土工程学报, 2002, 24(5): 626–628. (ZHENG 工 程 学 [32] 郑 报 2008 年 宏. 严格三维极限平衡法[J]. 岩石力学与工程学报, Hong, LI Chun-guang, Lee C F, GE Xiu-run. Finite element 2007, 26(8). (ZHENG Hong. A rigorous three-dimensional method for solving the factor of safety[J]. Chinese Jounal of limit equilibrium method[J]. Chinese Journal of Rock Geotechnical Engineering, 2002, 24(5): 626 – 628. (in Mechanics and Engineering, 2007, 26(8): 1529–1537. (in Chinese)) Chinese)) [25] 郑颖人, 赵尚毅. 岩土工程极限分析有限元法及其应用[J]. [33] 祝玉学. 边坡可靠性分析[M]. 北京: 冶金工业出版社, 土木工程学报, 2005, 38(1): 91–98,104. (ZHENG Ying-ren, 1993. (ZHU Yu-xue. Slope reliability analysis[M]. Beijing: ZHAO Shang-yi. Limit state finite element method for Metallurgical Industry Press, 1993. (in Chinese)) geotechnical engineering analysis and its applications[J]. [34] 葛修润. 用 PC 型微机对岩体工程课题进行有限元分析 China Civil Engineering Journal. 2005, 38(1): 91–98,104. [C]//第一届全国计算岩土力学研讨会论文集. 峨嵋: 西南 (in Chinese)) 交通大学出版社, 1987. (GE Xiu-run. The finite element [26] FELLENIUS W. Erdstatisch berechnungen[M]. Berlin, 1939. analysis on rock mass and engineering with PC[C]// [27] 陈祖煜. 土质边坡稳定分析——原理·方法·程序[M]. 北 Proceedings of symposium on the 1st National 京: 中国水利水电出版社, 2003. (CHEN Zu-yu. Earth slope Computational Mechanics on Rock and Soil. Emei: stability analyses—theory, method and programs[M]. Beijing: Southwest Jiaotong University Press, 1987. (in Chinese)) China Water Power Press, 2003. (in Chinese)) [35] GE Xiu-run, FENG Ding-xiang, GU Xian-rong, et al. [28] 中国科学院武汉岩体土力学研究所. 岩质边坡稳定性的 Stability and deformation analysis of complex rock 试 验 研 究 与 计 算 方 法 [M]. 北 京 : 科 学 出 版 社 , 1981. foundations of several large dams and hydropower stations in (Institute of Rock and Soil Mechanics, Chinese academy of China[C]// Proceedings of International Workshop on Rock sciences experimental study on rock slope stability analyses Foundation, 1995. and calculation methods[M]. Beijing: Science Press, 1981. (in Chinese)) [36] 刘艳章. 边坡与坝基抗滑稳定的矢量和分析法研究[D]. 北京: 中国 科 学院, 2007. (LIU Yan-zhang. Vector sum [29] 潘家铮. 建筑物的抗滑稳定和滑坡分析[M]. 北京:水利出 analysis method of slope and dam foundation stability against 版社, 1980. (PAN Jia-zheng. Stability against sliding of sliding[D]. Institute of Rock and Soil Mechanics, Chinese constructions and landslide analyses[M]. Beijing: China Academy of Sciences. 2007. (in Chinese)) Water Power Press, 1980. (in Chinese)) [37] 刘艳章, 葛修润, 李春光, 等. 基于矢量法安全系数的边 [30] 朱大勇, 丁秀丽. 三维边坡稳定准严格极限平衡解答[C]// 坡 与 坝 基 稳 定 性 分 析[J]. 岩 石 力 学 与 工 程 学 报, 2006, 三峡库区地质灾害与岩土环境学术研讨会. 重庆, 2006: 26(10): 2130 – 2140. (LIU Yan-zhang, GE Xiu-run, LI 166 – 177. (ZHU Da-yong, DING Xiu-li. Quasi-rigorous Chun-guang, et al. Stability analysis of slope and foundation limit equilibrium solutions of 3D slope stability[C]// based on vector method safety factor[J]. Chinese Journal of Proceeding of symposium on geological hazards and Rock Mechanics and Engineering, 2007, 26(10): 2130–2140. Geotechnical Environmental Problems in Three-Gorges (in Chinese)) Reservoir Areas. Chongqing, 2006: 166–177. (in Chinese)) [38] 刘艳章, 葛修润, 王水林, 等. 高密度电法在三峡库区滑 宏, 谭国焕, 刘德富. 边坡稳定性分析的无条分法[J]. 坡 勘 察 中 的 应 用 [J]. 岩 土 力 学 ， 2006, 27( 增 ). (LIU 岩土力学, 2007, 28(7): 1285–1291. (ZHENG Hong, THAM Yan-zhang, GE Xiu-run, WANG Shui-lin, et al. Application Leslie George, LIU De-fu. A slice-free method for stability of high density resistivity method to landslide survey in analysis of slopes[J]. Rock and Soil Mechanics, 2007, 28(7): Three-Gorges Reservoir Areas[J]. Rock and Soil Mechanics. 1285–1291. (in Chinese)) 2006, 27(S). (in Chinese)) [31] 郑